Действия с матрицами

Рассмотренные выше операции над массивами были реализованы исходя из предположения, что массивы имеют одну размерность. Но существует группа задач, в которой работа осуществляется с массивами большей размерности. Прежде всего это действия с матрицами. Кстати, такая структура данных, как сеть (или граф) представляется с помощью матрицы.

Дека

Дека — очередь с двумя концами. Дека является последовательным списком, в котором включение и исключение элементов может осуществляться с любого из двух концов списка. Логическая и физическая структуры деки аналогичны обычной очереди, но относительно деки следует говорить не о хвосте и голове, а о правом и левом конце очереди. Реализацию операций включения и исключения в деку следует также дополнить признаками левого или правого конца. В литературе можно встретить понятие дека с ограниченным вводом. Это дека, в которой элементы могут вставляться в одном конце, а удаляться с обоих.

Дерево

То, что неясно, следует выяснить. То, что трудно творить, следует делать с великой настойчивостью.

Конфуций Деревом называется сетевая структура, обладающая следующими свойствами:

среди всех узлов существует один, который не имеет ребер, входящих от других узлов, — этот узел называется корнем;

все узлы, за исключением корня, имеют одно и только одно входящее ребро;

ко всем узлам дерева имеется путь, начало которого лежит в корне дерева. Графически дерево изображают так, как показано на Рисунок 2.18.

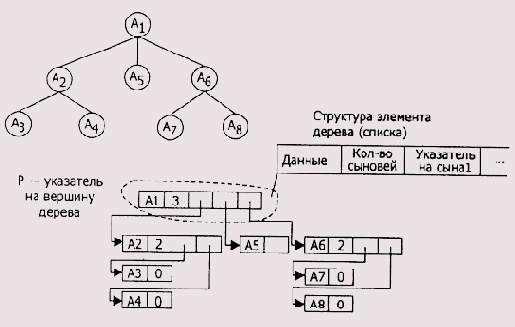
Рисунок 2.18. Изображение дерева и соответствующего ему связного списка

Следуя терминологии дерева, можно ввести некоторые определения, касающиеся его структуры. Ребра, соединяющие смежные узлы дерева, называются ветвями. Оконечные узлы дерева, которые не ссылаются на другие узлы, называются листьями. Другие узлы дерева, за исключением корня, называются узлами ветвления. Две смежные вершины дерева состоят в «родственных» отношениях. Вершина X, находящаяся на более высоком уровне дерева по отношению к вершине Y, называется отцом. Соответственно, вершина Y по отношению к X называется сыном. Если вершина X имеет несколько сыновей, то по отношению друг к другу последних называются братьями. В принципе, вместо этих терминов можно использовать следующие: родитель, потомок и т. п. Классификация деревьев производится по степени исхода ветвей из узлов деревьев. Дерево называется m-арным, если степень исхода его узлов не превышает значения m.

В практических приложениях широко используется специальный класс деревьев — бинарные деревья. Бинарное дерево — m-арное дерево при m = 2. Это означает, что степень исхода его вершин не превышает 2. В случае когда m равно 0 или 2, имеет место полное бинарное дерево. Важно то, что любое m-арное дерево можно преобразовать в эквивалентное ему бинарное дерево. В свою очередь, в силу ограничений по степени исхода вершин бинарное дерево легче представлять в памяти и обрабатывать. По этой причине мы основное внимание уделим работе с бинарными деревьями.

Перечислим операции, которые обычно выполняются при работе с деревьями:

представление дерева в памяти;

обход или прохождение дерева (поиск в дереве);

включение в дерево и исключение из дерева определенного узла;

балансировка дерева и операции со сбалансированным деревом.

Двусвязные списки

Двусвязный список представляет собой список, связующая часть которого состоит из двух полей. Одно поле указывает на левого соседа данного элемента списка, другое — на правого. Кроме этого, со списком связаны два указателя — на голову и хвост списка (Рисунок 2.13, сверху). Более удобным может быть представление списка, когда функции этих указателей выполняет один из элементов списка, одно из полей связи которого указывает на последний элемент списка (Рисунок 2.13, снизу).

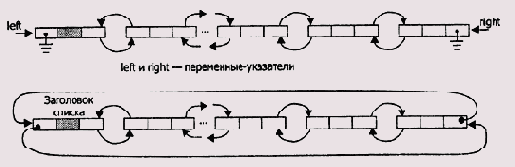
Рис 2.13. Схемы организации двухсвязных списков

Преимущество использования двусвязных списков — в свободе передвижения по списку в обоих направлениях, в удобстве исключения элементов. Возникает вопрос о том, как определить начало списка. Для этого существуют по крайней мере две возможности: определить два указателя на оба конца списка или определить голову списка, указатели связей которой адресуют первый и последний элемент списка. В случае двусвязного списка добавление и удаление

start proc near :точка входа в программу ,

:вывод строки текста - приглашение на ввод сроки для инвертирования :вводим строку текста для инвертирования

.-создаем связанный список, для чего инициализируем заголовок списка

create_doubly_li st Doubly_Head_l i st :вводим символы строки с клавиатуры до тех пор. пока не встретится "."

lea esi.mas cycl: mov al .[esi]

cmpal.V

je rev_out

add_li st i tem_l i st.Doubly_Head_li st.Hand_Head

mov [ebx].info.al

incesi

jmp cycl rev_out: ;вывод строки в обратном порядке

mov esi.offset mas_rev

mov ebx.DoublyJHeadJ i st. 1 ast cycl2: mova 1 .[ebx].info

mov [esi].al

incesi

mov ebx,[ebx].prev

cmp [ebx].info.Offh :дошли до последнего элемента списка"?

jnecycl2

:выводим инвертированную строку на экран :......

Включение в список

Для включения нового элемента в список необходимо предварительно локализовать элемент, до или после которого будет производиться это включение. Для того чтобы включить новый элемент после локализованного, то есть справа, необходимо выполнить действия, отраженные фрагментом кода:

itemjist struc ; элемент списка

prev dd 0 :адрес предыдущего элемента

info db 0 содержательная часть (в нашем случае - символ)

next dd 0 :адрес следующего элемента

ends

;предполагаем, что адрес локализованного элемента находится в регистре ЕВХ.

:а адрес нового элемента - в ЕАХ

push [ebx].next

pop [eax].next :[ebx].next->[eax].next mcv [eax].prev.ebx;адрес предыд. эл-та->[еах].ргеу mov [ebx].next.eax:адрес след. эл-та->[еЬх].пех1

:будьте внимательны - меняем указатель предыд. эл-та в следующем за новым элементом mov ebx.[eax].next;адрес след. эл-та-KebxJ.next mov [ebx].prev.eax;адрес предыд. эл-та->[еЬх].ргеу

Включение элемента перед локализованным выполняется аналогично. Простота работы с двусвязными списками в отличие от односвязных достигается за счет отсутствия проблем с передвижением по списку в обе стороны.

Исключение из списка

Аналогично включению, исключение из двусвязного списка не вызывает проблем и достигается перенастройкой указателей. Фрагмент программы, демонстрирующей эту перенастройку, показан ниже.

itemjist struc ;элемент списка

prev dd 0 ;адрес предыдущего элемента

info db 0 содержательная часть (в нашем случае - символ)

next dd 0 -.адрес следующего элемента

ends

предполагаем, что адрес локализованного элемента находится в регистре ЕВХ

mov eax.[ebx].prev;адрес предыд. эл-та->еах

push [ebx].next

pop [eax].next

mov eax.[ebx].next ;адрес следующ. эл-та->еах

push [ebx].prev

pop [eax].prev

В общем случае одно- и двусвязные списки представляют собой линейные связанные структуры. Но в определенных случаях второй указатель двусвязного списка может задавать порядок следования элементов, не являющийся обратным по отношению к первому указателю (Рисунок 2.14).

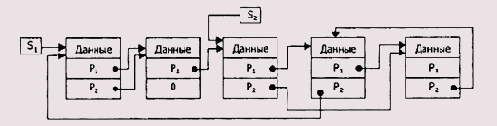
Рисунок 2.14. Логическая структура нелинейного двусвязного списка

Формальное описание языка программирования

Язык программирования является подмножеством естественного языка и предназначен для поддержки процесса общения человека с компьютером. В общем случае язык — это множество предложений, которые можно записать на нем. Отличие языка программирования от естественного — в его законченности или замкнутости. Под этим понимается, что теоретически можно перечислить все предложения, которые можно на нем составить. Для естественного языка это невозможно. В контексте нашего изложения под языком программирования будем понимать не только языки высокого уровня, но и языки командных процессоров и вообще любые наборы предложений, с помощью которых производится управление работой некоторой программы.

Теория компиляции базируется на том, что любой язык может быть описан формально.

Основа любого естественного языка — его алфавит, то есть множество символов букв. Вспомним, что обучение в школе начинается с букваря, то есть со знакомства с набором символов, из которых в дальнейшем будут строиться слова. Приступая к изучению языка программирования, программист также вначале знакомится с набором символов (букв, цифр, разделительных знаков), из которых строятся слова программы и объединяются затем в предложения программы. Для формального описания языка программирования также необходимо знать алфавит, но в этом случае его понятие отличается от того, к которому мы привыкли. К этому мы вернемся чуть позже. Для написания программы недостаточно знать только лишь один алфавит. Так, в школе после изучения алфавита дети начинают изучать предмет «Русский язык». Можно выделить по крайней мере две цели, которые при этом ставятся: во-первых, на основе алфавита и набора правил научить школьника правильно строить слова языка (которые составляют его лексику); во-вторых, научить его правильно составлять предложения из слов, то есть делать это так, чтобы его могли понимать окружающие. Для построения правильных предложений в любом языке существует набор правил, которые описывают синтаксис этого языка. Каждому правильному предложению языка приписывается некоторый смысл. Описание смысла предложений составляет семантику языка.

и ту же мысль можно

Естественный язык многозначен, и часто с его помощью одну и ту же мысль можно выразить несколькими синтаксически разными предложениями. Компьютер — не человек, и общение с ним (во всяком случае, пока) должно быть однозначным, то есть не может быть двух разных по написанию предложений, выполняющих одно действие. Применительно к компьютеру семантика языка программирования представляет собой описание того, как следует исполнять на машине конкретное предложение. Различие синтаксиса и семантики лучше всего иллюстрирует следующий классический пример. Имеются два одинаковых с точки зрения синтаксиса предложения:

Здесь I, J, К — целые, а X, Y, Z — вещественные числа. В машинном представлении для вычисления данных выражений будут использоваться не только разные команды, но и алгоритмы. Если вдруг перед нами будет поставлена задача перевода программы на другой язык программирования, то в той или иной степени будет меняться все — алфавит, лексика, синтаксис, но семантика в идеале должна остаться неизменной.

Таким образом, для формального описания языка необходимы по крайней мере два элемента — алфавит и набор правил (синтаксис) — для построения предложений языка. Существует еще несколько элементов формального описания, которые также важны для процесса однозначного построения и распознавания предложений языка. Знакомство с ними целесообразно вести в рамках такого понятия, как грамматика языка.

Грамматика языка представляет собой механизм порождения предложений языка и определяет форму (синтаксис) допустимых предложений языка. Это важное положение, запомните его. В своем изложении мы постараемся по возможности избежать «формализмов», которыми изобилует теория компиляции, хотя полностью сделать это нам не удастся. В частности, без этого трудно ввести понятие грамматики. Формально грамматику языка G можно определить как совокупность четырех объектов: G-{Vt. Vn. P. Z}

Эти объекты можно описать следующим образом.

Vt — множество терминальных символов грамматики. Кстати, в этом контексте слово «символ» не означает отдельную литеру. В контексте терминальных и нетерминальных символов символы — это ключевые слова, допустимые имена идентификаторов, знаки операций, разделительные знаки, то есть все отдельные объекты исходного текста программы, имеющие смысл для компилятора. По сути, множество терминальных символов представляет собой набор лексем, которые являются допустимыми словами языка, составляющими его лексику. Таким образом, важно понимать, что исходный текст программы состоит только из терминальных символов.

Vn — множество нетерминальных символов. Эти символы являются вспомогательными конструкциями, определенными внутри грамматики. К пояснению того, что представляют собой нетерминальные символы, мы вернемся чуть позже. Важно отметить, что множества Vt и Vn не пересекаются. Объединение множеств Vt и Vn составляет алфавит языка. Отметим, что введенное здесь понятие алфавита грамматики (а значит, и языка) отличается от того, что есть в букваре. Не забывайте об этом важном моменте при проведении дальнейших аналогий.

P- набор правил грамматики, определяющих синтаксис языка. Эти правила называются правилами вывода. Эти правила определяют возможность получения любого предложения языка.

Z- начальный символ языка. Он входит в множество Vn. Одна из его особенностей состоит в том, что он должен встретиться по крайней мере в левой части одного из синтаксических правил, входящих в множество Р. И именно это правило является первым в процессе вывода любого допустимого предложения языка.

Далее, если не оговорено особо, прописными буквами будем обозначать терминальные символы, а строчными — нетерминальные.

Поясним, как с помощью грамматики задается язык. Начнем с простого примера. Опишем грамматику G1nt языка целых чисел:

Glnt = {Vt=(0.1.2,3.4.5.6.7.8.9). VrH число, цифра). Р. г=(число)}.

Множество правил Р грамматики Gint выглядит так:

число::=цифра

число::=цифра число

цифра::=0

цифра::=1

цифра::=2

цифра::-3

цифра::=4

цифра::=5

цифра::=6

цифра::-7

цифра::-8

цифра::=9

Обычно подобные правила записывают короче:

число::= цифра | цифра число цифра::=0|1|2|3|4|5|6|7|8|9

Здесь символ | означает альтернативу выбора, при этом все элементы, которые он разделяет, равноправны по отношению к нетерминальному символу левой части. Покажем, что эта простая грамматика действительно однозначно определяет язык, с помощью которого можно получить любое целое число. Процесс получения предложения языка, задаваемого грамматикой, называется выводом и определяется правилами вывода, входящими во множество Р. Причем начинать вывод предложения можно не с любого правила, а только с одного из тех, в левой части которых стоит начальный символ языка Z. В нашем случае таким символом является нетерминальный символ число. Видно, что он стоит в левой части двух правил:

число::= цифра (2.9)

число::= цифра число (2.10)

Сам процесс вывода предложения языка итеративный и состоит из одного или нескольких шагов. Например, рассмотрим процесс получения предложения 8745. Согласно сказанному выше, на первом шаге вывода можно использовать правило (2.9) или (2.10). Если использовать правило (2.9), то это означает, что предложение будет состоять из одной цифры. В нашем случае на первом шаге необходимо применить правило (2.10). Производя дальнейшие подстановки, можно получить предложение, состоящее из любого количества цифр. Заметьте, что на последнем шаге вместо правила (2.10) применяется правило (2.9), что в конечном итоге приводит к желаемому результату. Таким образом, предложение 8745 получается использованием правил вывода грамматики в следующей последовательности:

число => цифра число => 8 число => 8 цифра число => 87 число => 87 цифра число => 874 число => 874 цифра => 8745.

Важно отметить, что вывод предложения заканчивается лишь в том случае, если в нем содержатся только терминальные символы. Если этого сделать не удается, то это означает одно — целевое предложение недопустимо в этом языке. Для того чтобы отличить предложение, соответствующие промежуточному выводу, от конечного предложения, можно следовать общепринятой терминологии. В соответствии с нею любая строка терминалов и нетерминалов, которая получается из начального символа языка, называется сентенциальной формой. Предложением называется сентенциальная форма, не содержащая нетерминальных символов.

Для нашего примера сентенциальными формами являются все строки, которые получаются в процессе вывода:

цифра число, 8 число, 8 цифра число, 87 число, 87 цифра число, 874 число, 874 цифра, 8745.

Предложением языка является только одна из этих сентенциальных форм — строка 8745.

На правила грамматики обычно накладываются определенные ограничения. В зависимости от этих ограничений языки делятся на 4 класса.

Класс 0. Грамматики без ограничений. Правила этих грамматик имеют форму: u=>w. При этом не накладывается каких-либо ограничений на строки и и v в левой и правой частях правил вывода. Используя языки этого класса, можно моделировать естественный язык.

Класс 1. Контекстно- чувствительные грамматики. Правила этих грамматик имеют форму: AuB=>AwB. Замена и на v возможна лишь в контексте строк А и В (отсюда и название). При этом: ueVn; we(VnuVt)*; A, Be(VnuVt)+. Символы * и + обозначают множество всех строк, выводимых в рамках данной грамматики, включая ("*") и исключая ("+") пустую строку.

Класс 2. Контекстно-свободные, или контекст}ю-нечувствительные, грамматики. Их правила имеют форму: u=>w, где ueVn, we(VnuVt)*. Название данного класса грамматик отражает тот факт, что и можно заменить на w, не обращая внимания на контекст. Другая особенность грамматик этого класса в том, что в правой части всех правил грамматики стоит только один нетерминал. Отметим, что языки программирования моделируются с использованием грамматик именно этого класса.

Класс 3. Регулярные, или автоматные, грамматики. Исходя из вида правил, которые используются в таких грамматиках, их делят на два подкласса.

Грамматика, выравненная вправо. Ее правила имеют форму: u=>Aw или и=>А, где AeVt, u и weVn.

Грамматика, выравненная влево. Ее правила имеют форму: u=>\vA или и=>А, где AeVt, u и weVn. Это очень важный класс грамматик, который наряду с грамматикой класса 2 используется для моделирования языков программирования. Заметим, что рассмотренная выше грамматика языка целых чисел как раз и является грамматикой класса 3. Чтобы убедиться в этом, необходимо лишь немного подправить правила:

число: ."¦ цифра

число: :*=0 число |1 число |2 число |3 число |4 число |5 число |б число |7 число

|8 число |9 число иифра::=0|1|2|3|4(5|6|7|8|9

Приведенная выше классификация языков была введена в 1959 году американским ученым-лингвистом Н. Хомским.

Выше, при изложении основ работы с двусвязными списками, мы ввели понятие конечного автомата. Язык, который воспринимает любой конечный автомат, относится к языкам класса 3, то есть является регулярным. Покажем это, сформулировав грамматику для языка вещественных чисел. Напомним соответствующее регулярное выражение: (+| -)dd*.dd*e(+| 0dd*, где d* обозначает цифру 0-9 или пусто.

Grea1-{Vt-(.. + . -. е. 0. 1, 2, 3. 4. 5. 6. 7. 8. 9). VrHreal. s. m, n. k, t). P. Z-(< real >)}.

Множество правил P грамматики Greal:

real=>+s|-s|Ds s=>ds |. m m=>Dn | D n=>Dn | ek k=>+t|-t|Dt|D T=>dT|d

Попробуйте, используя данную грамматику, самостоятельно вывести следующие предложения языка вещественных чисел: 5.5, +0.6е-5. Покажите, что предложение «+.45е4» невыводимо в терминах данной грамматики. При необходимости посмотрите еще раз материал раздела «Сеть» данной главы, где было введено понятие конечного автомата и разработана программа, моделирующая его работу при распознавании строки с вещественным числом.

Анализ правил вывода грамматики Greal показывает, что генерируемый ею язык относится к языкам класса 3, а сама грамматика является грамматикой, выровненной вправо.

Рассмотрим еще одну грамматику для языка идентификаторов Gident.

G1dent-{Vt-(.. +. -. е. 0. 1. 2. 3. 4. 5. 6. 7. 8, 9). VrHreal. S. M. N. К. Т), Р, 2=(< real >)}

Множество правил Р грамматики Gident:

ident=>letter| ident letter | ident figure letter => A|B|C| ... X|Y|Z figure => 0|l|2|...8|9

Видно, что это тоже грамматика языка класса 3.

А теперь приведем пример грамматики, генерирующей язык класса 2. С ее помощью смоделируем псевдоязык, похожий на Pascal, который мы используем в нашей книге для пояснения некоторых алгоритмов:

Vt=(riPOrPAMMA, ПЕРЕМЕННЫЕ, НАЧ_ПРОГ. КОН_ПРОГ, НАЧ_БЛОК. КОН_БЛОК. ".".ID. CHJNT. СН_ REAL. «:».«:». «/». REAL. INTJYTE. INT_WORD. INT_OWORD. «,».«:»». «=».«+».«-».«*». DIV. MOO. «(». «)». «[». «]». «<».«>», «==»,«>=».«=<». ЧИТАТЬ, ПИСАТЬ, ДЛЯ. ДОДЕЛАТЬ. ПОКА. Д08НИЗ, ЕСЛИ. ЕСЛИ. ДО. ТО. ПЕРЕЙТИ_НА. ПОВТОРИТЬ),

Vn»( prog, prog-name, dec-list, stmt-list, dec. id-list, type. var. varjnd. ind. label. go_to. stmt, assign, read, write, until, for. call_func. exp. term, factor, index-exp. body, condition. cond_op). P. Z-(< prog >) }

Множество правил Р грамматики G:

prog => ПРОГРАММА prog-name ПЕРЕМЕННЫЕ dec-list НАЧ_ПРОГ stmt-list КОН_ПРОГ

prog-name => ID

dec-list => dec | dec-list : dec

dec => type id-list

type => INTJYTE | INT_WORD | INT_DWORD | REAL

1d-list=> var | id-list , var

var=> ID | varjnd

var_ind=> ID ind

ind => [ exp ]

stmt-list => stmt | stmt-list ; stmt

stmt => assign | read | write | for | while | until | label | go_to | cond op | call_

func

assign => var :- exp exp => term | exp + term | exp - term

term => factor | term * factor | term DIV factor| term MOD factor factor => var | CH_INT | CH_REAL | ( exp ) read => ЧИТАТЬ (id-list) ~ write => ПИСАТЬ (id-list) for=> ДЛЯ index-exp ДЕЛАТЬ body until => ПОВТОРИТЬ body ПОКА logical_exp call_func => ID (id-list) cond_op=> ЕСЛИ logical_exp TO body while => ПОКА logical_exp ДЕЛАТЬ body label => ID : stmt-list go_to => ПЕРЕЙТИ_НА idjabel idjabel => ID

index-exp => var := exp ДО exp | exp Д0ВНИЗ exp logical_exp => ( condition )

condition => l_exp < l_exp | l_exp <@062> l_exp | l_exp >- l_exp | l_exp =< l_exp | l_exp — l_exp | l_exp ИЛИ l_exp | l_exp И l_exp | l_exp XOR l_exp | HE l_exp l_exp => exp | condition body => stmt | НАЧ_БЛОК stmt-list КОН_БЛОК

Посмотрим внимательно на правило вывода, в левой части которого стоит начальный символ языка prog. Правая часть этого правила представляет собой сентенциальную форму, содержащую все необходимые элементы программы. На примере этой грамматики хорошо видно, что представляет собой алфавит языка программирования. По сути это совокупность лексем, которые программист использует для написания программы и которые в терминах языка являются терминальными символами, а также нетерминалов, которые имеют смысл в рамках грамматики. Более того, к терминальным символам относятся также символы ID (идентификатор), CHINT (целое число) и CHREAL (вещественное число). В программе им соответствуют Совершенно разные сочетания символов букв, цифр и разделительных знаков, например идентификаторы — chl, sab, masl; целые числа — 1, 24, 98584; вещественные числа — +33.5, 0.95е-3. С точки зрения синтаксиса эти разные по написанию объекты являются терминальными символами — идентификатором, целым числом, вещественным числом. Это ключевой момент. Мы

к нему еще вернемся, а пока давайте посмотрим, каким превращениям подвергается исходный текст программы, для того чтобы превратиться в форму, пригодную для машинного исполнения.

Сложные структуры данных

Глава 2. Сложные структуры данных

Элементы компиляции программ

Большинство людей считают компьютеры математическими машинами,

разработанными для выполнения численных расчетов. В действительности

же компьютеры представляют собой языковые машины: основа их

могущества заключается в способности манипулировать лингвистическими

знаками — символами, которым приписан некоторый смысл.

Терри Виноград

В процессе изложения материала данного раздела мы получили достаточные знания для того, чтобы с пользой применить их на примере достаточно сложной задачи. Одной из таких задач традиционно считается разработка компилятора (интерпретатора). Тем более что у нас есть для этого повод — необходимость создания препроцессора для новых команд микропроцессоров Pentium Pro/II/IH/IV (см. главу 10). Исходя из этого задачу будем решать поэтапно: на первом этапе разберемся с общими вопросами из теории компиляции, которые будут полезны в контексте решения нашей задачи, а затем, на втором этапе, разработаем сам препроцессор. В соответствии с этими этапами весь материал также будет разбит на две части и рассмотрен в разных главах настоящей книги. Но для того, чтобы все наше строение было логически связанным, мы сформулируем для каждого из этапов свои целевые установки. Цель первого этапа — научиться проводить распознавание и синтаксический разбор одиночных предложений, принадлежащих некоторому языку. Цель второго этапа — применить полученные знания для обработки некоторой программы на языке ассемблера, содержащей новые команды микропроцессоров Pentium Pro/II/III, о которых транслятор ассемблера «не знает». В результате этой обработки новые команды будут замещены эмулирующим кодом. Конечно, кто-то возразит — можно попытаться достать соответствующий «patch» к транслятору, что позволит ему непосредственно поддерживать новые команды. Или выбрать другой путь — использовать набор макрокоманд, предоставляемых фирмой Microsoft (защищенный, кстати, ее авторскими правами). Но, как быть тем, кто привык работать с ассемблерами других фирм? Более того, разработка данной задачи и использование ее результатов в своей практической работе ощутимо поднимает уровень профессиональной подготовки программиста. А это уже достижение одной из целей данной книги.

Теория компиляции разработана очень хорошо. В списке литературы вы сможете найти ссылки на некоторые источники, где приведено ее описание. Наша задача — сформировать некий подход, который бы на хорошем профессиональном уровне позволил вам решать определенный круг задач. Конечно же, мало кому придется разрабатывать свой транслятор, но практически всем приходилось или придется разрабатывать языковой интерфейс своей программы с пользователем. Ну и как ваша программа будет его обрабатывать? На основе каких-то символьных заготовок? Изучив предлагаемый материал, вы, например, самостоятельно сможете производить синтаксический разбор предложений, поступающих

на вход вашей программы, оптимальным образом анализировать содержимое нужных файлов и т. п.

Лексический анализ

Цель лексического анализа — выделение и классификация лексем в тексте исходной программы. Программа, которая выполняет лексический анализ, называется сканером, или лексическим анализатором. Сканер производит посимвольное чтение файла с исходным текстом программы.

Полный набор лексем языка определен множеством терминальных символов в его грамматике. Среди них можно выделить изменяемые и неизменяемые лексемы. Неизменяемые лексемы в любой программе пишутся одинаково. Для грам-

матики псевдоязыка это такие лексемы, как: ПРОГРАММА, ПЕРЕМЕННЫЕ, НАЧ_ПРОГ, КОН_ ПРОГ, НАЧ_БЛОК, КОН_БЛОК, «.», «;», «:», «/», REAL, INTBYTE, INT_WORD, INTDWORD, «,», «:=», «=», «+», «-», «*», DIV, MOD, «(», «)», «[», «]», «<», «>», «==», ЧИТАТЬ, ПИСАТЬ, ДЛЯ, ДОДЕЛАТЬ, ПОКА, ДОВНИЗ, ЕСЛИ, ЕСЛИ, ДО, ТО, ПЕРЕЙТИ_НА, ПОВТОРИТЬ. «За бортом» остались три терминальных символа — ID, CH_INT, CH_REAL. Эти терминальные символы соответствуют идентификаторам, целым и вещественным числам. Естественно, что даже в пределах одной программы они будут различны. Задачей сканера как раз и является распознавание изменяемых и неизменяемых терминальных символов. С позиции логики обработки сканером удобно все терминальные символы отнести к одному из следующих классов (применительно к нашей грамматике псевдоязыка):

идентификаторы — ID;

ключевые слова - ПРОГРАММА, ПЕРЕМЕННЫЕ, НАЧПРОГ, КОН_ПРОГ, НАЧБЛОК, КОН_ БЛОК, REAL, INTJYTE, INTWORD, INT_DWORD, DIV, MOD, ЧИТАТЬ, ПИСАТЬ, ДЛЯ, ДОДЕЛАТЬ, ПОКА, ДОВНИЗ, ЕСЛИ, ЕСЛИ, ДО, ТО, ПЕРЕЙТИ_НА, ПОВТОРИТЬ;

целые числа — CHINT;

вещественные числа — CH_REAL;

однолитерные разделители — «.», «,», «;», «:<@187>, «+»,«-», «*»,«/», «(»,«)», «=», «[», «]», «<», «>»;

В двулитерные разделители — «:=», «=», «>=», «=<».

Задача сканера — построить для каждого терминального символа его внутреннее представление. Делается это для того, чтобы убрать лишнюю информацию, подаваемую на вход синтаксического анализатора. Проведем аналогию. Все знают о твердом порядке слов в английском предложении. При этом не оговариваются конкретные слова, которые должны стоять на месте подлежащего, сказуемого, дополнения. Главное, чтобы слово, которое стоит, например, на месте подлежащего, было существительным или местоимением, то есть относилось к определенному классу. Сканер как раз и выполняет классификацию лексем, подаваемых на его вход. Он распознает, например, что очередная лексема является ключевым словом begin, после чего присваивает ей определенное целое значение и передает его далее. Если же сканер распознал на своем входе некоторый идентификатор, то он производит не просто замещение, но и некоторые другие действия. Чтобы подробнее разобраться со всем этим, необходимо понять состав и назначение структур данных, определенных внутри сканера.

Сканер работает с определенным набором таблиц, среди которых есть входные и выходные.

В общем случае сканер должен иметь две входные таблицы — таблицу лексем языка и таблицу классов литер. Таблица лексем языка содержит перечень всех лексем языка и соответствующих им целочисленных значений. Для нашей грамматики таблица может быть следующей:

Лексема	Внутренний код	Лексема	Внутренний код
ПРОГРАММА	1	*	23
		:=	24
НАЧ БЛОК	3	)	25
КОН_БЛОК	4	НАЧ_ПРОГ	26
REAL	5	КОН_ПРОГ	27
INT_BYTE	6	/	28
DIV	7	INT_WORD	29
ЧИТАТЬ	8	INT_DWORD	30
ПИСАТЬ	9	=	31
ДЛЯ	10	MOD	32
ДЕЛАТЬ	11	[	33
(	12	]	34
ТО	13	<	35
ID	14	>	36
CHJNT	15	==	37
CH_REAL	16	>=	38
	17	=<	39
>	18	до	40
1	19	ПОКА	41
•	20	довниз	42
+	21	ЕСЛИ	43
-	22	до	44
		ПЕРЕЙТИ_НА*

Таблица классов литер используется только в процессе сканирования и предназначена для выяснения класса литеры, когда она выбирается сканером из входного потока. Лучше всего эту таблицу организовать в виде массива, элементы которого отражены на используемую кодовую таблицу (например, таблицу ASCII). Значение каждого элемента таблицы классов литер определяется классом литеры в кодовой таблице. В общем случае можно определить следующие классы литер:

d - цифра;

1 — буква;

b — литеры, которые игнорируются, к ним может относится, например, пробел;

s1 — одиночные разделители: «.», «:», «(«, «)», «*»;

s2 — особые одиночные разделители: «.», «+», «-»,«:», «=», «<», «>».

Последние разделители отличаются тем, что они могут быть как собственно одиночными разделителями, так и входить в состав литер лексем, состоящих из нескольких литер. Например, разделитель «:» является не только одиночным, но и первой литерой двухлитерного разделителя «:=», а литеры «.», «+» и «-» являются составной частью лексемы «вещественное число».

Количество выходных таблиц может быть различным и определяется сложностью входного языка. В минимальном варианте используют две или три таблицы: таблицу лексической свертки, таблицу идентификаторов и, возможно, таблицу констант. Рассмотрим пример программы на псевдоязыке:

ПРОГРАММА progl (1M14, #progl) ПЕРЕМЕННЫЕ (2)

INTBYTE 1 (6) (14. #i)

НАЧ_ПРОГ (26)

ДЛЯ i := О ТО 9 ДЕЛАТЬ (10Н14, #i)(24)(15. 0)(13)(15. 9Н11) ПИСАТЬ (i) (9)(12)(14, #i)(25)

КОНПРОГ (27)

Приведенная программа выводит на экран целые числа от 0 до 9, хотя в контексте нашего обсуждения это и не важно. После обработки сканером исходный текст программы преобразуется во внутреннее представление, которое показано справа для каждой строки. Становится понятным значение термина «лексическая свертка» — программа как бы сворачивается в некоторую унифицированную форму, теряя при этом свою индивидуальность. Каждая лексема замещена своим кодом. Идентификаторы замещены кортежами, первый элемент которых является кодом лексемы-идентификатора, а второй элемент — ссылкой на элемент таблицы идентификаторов, где содержится более подробная информация о данном идентификаторе. Ссылка может быть адресом элемента в таблице, но может быть удобнее, чтобы это было просто число, представляющее собой индекс в этой таблице. Это же касается и лексемы «целое число». Здесь возможны разные варианты: во-первых, можно организовать таблицу констант, подобную таблице идентификаторов; во-вторых, для простых применений константу можно разместить прямо в кортеже. В нашем примере для констант выбран второй вариант.

Можно предложить несколько способов организации таблицы идентификаторов. Самый простой и неэффективный — в виде массива указателей на списки переменной длины, элементы которого содержат символы идентификатора. Имена идентификаторов нужны лишь на этапе лексической свертки для выделения одинаковых идентификаторов. Важно понимать, что после выделения сканером идентификаторов и присвоения одинаковым из них ссылок на определенный элемент массива (таблицы) идентификаторов сами символьные имена уже не нужны. Если, конечно, не будет производиться формирование диагностических сообщений. Впоследствии эти указатели можно переориентировать для ссылок на ячейки с другой информацией, например с адресом области памяти, которая будет выделена для данного идентификатора на этапе генерации кода. Аналогично можно организовать и таблицы констант, если в этом возникнет необходимость. Это самые простые варианты организации подобных таблиц. Но исходя из опыта, полученного при изучении материала данной книги, можно организовать таблицу символов более эффективно — в виде лексикографического дерева или используя методы хэширования. Если используется лексическое дерево, то каждый узел этого дерева может состоять из следующих полей:

уникальный номер — номер, который на последующих этапах трансляции

будет идентифицировать данное символьное имя;

указатель на список, содержащий символы идентификатора;

указатель на список с номерами строк, в которых встретился данный идентификатор.

Впоследствии, когда имена идентификаторов не будут нужны, можно на основе этого дерева построить хэш-таблицу, доступ к элементам которой будет осуществляться на основе уникальных номеров. Кстати, для повышения эффек-

тивности процесса распознавания стоит все терминальные символы — ключевые слова языка, разделители и т. п. (за исключением id, chint и ch_rea1) — также свести в отдельное лексикографическое дерево или организовать хеш-таблицу.

Можно поступить по-другому. Этот вариант, который можно использовать для анализа ввода в командной строке и т. д., работает в случае, если сканер вызывается из синтаксического анализатора. Суть его в том, что сканер вызывается из синтаксического анализатора, когда последнему нужна очередная лексема. Сканер выделяет ее во входном потоке и выдает синтаксическому анализатору кортеж из двух элементов: кода лексемы и строки, содержащей саму лексему.

А как организовать сам процесс распознавания лексем входной программы? Для этого попробуем сформулировать некий обобщенный алгоритм построения сканера.

1. Выделить классы лексем.

2. Определить классы литер.

3. Определить условия выхода из сканера для каждого класса лексем.

4. Для каждого класса лексем поставить в соответствие грамматику класса 3.

5. Для каждой грамматики, построенной на шаге 4, построить конечный автомат, который будет распознавать лексему данного класса.

6. Выполнить объединение («склеивание») конечных автоматов для всех классов лексем.

7. Составить матрицу переходов для «склеенного» конечного автомата.

8. «Навесить» семантику на дуги «склеенного» конечного автомата.

9. Выбрать коды лексической свертки для терминалов грамматики и формат таблицы идентификаторов.

10. Разработать программу сканера.

Полностью реализовывать этот алгоритм для сканера транслятора упрощенного языка Паскаль мы не будем. Это не является предметом нашей книги. Нас интересуют прежде всего организация данных и возможности по работе с ними на ассемблере. Поэтому, для того чтобы пояснить подход к подобным задачам, мы остановим свое внимание на шагах 1-8 приведенного алгоритма.

Лексикографическое дерево

Деревья поиска, подобные лексикографическим, являются альтернативой методам поиска, основанным на хэшировании. Структурно лексикографическое дерево представляет собой бинарное дерево поиска. Рассмотрим задачу, которая заключается в анализе некоторого текстового файла и сборе статистики о частоте встречаемости слов в этом тексте. В качестве итога требуется вывести на экран информацию о частоте встречаемости каждого слова. В такой постановке задачи программа будет состоять из следующих частей.

Чтение текстового файла и построение соответствующего ему лексикографического дерева. Для этого будем читать и проверять на предмет новизны каждое слово в анализируемом тексте. Если слово встретилось впервые, то необходимо сформировать и внести в дерево узел, который структурно состоит из двух полей: поля для хранения самого слова и поля для хранения частоты встречаемости этого слова в тексте.

Для вывода на экран статистики необходимо совершить левосторонний обход дерева. Если изменить условия вывода статистики, например упорядочить слова по частоте встречаемости в тексте, то необходимо выполнить перестроение дерева и его последующий правосторонний обход.

Для простоты преобразования положим, что каждое слово может встречаться в тексте не более 9 раз. Длина слова — не более 10 символов (для экономии места контроль количества вводимых символов не производится). Слова в файле разделяются одним пробелом. Также для сокращения текста программы считаем, что имя входного файла фиксировано — in.File.txt.

Программа построения лексикографического дерева prg_12_78.asm имеет достаточно большой размер, в связи с чем ее текст вынесен на дискету.

Бинарные деревья — не единственный вид деревьев, которые могут быть использованы в ваших программах. В литературе можно ознакомиться с представлениями деревьев, отличных от бинарных. Мы не будем развивать далее проблему представления деревьев, хотя, честно говоря, очень хочется. За кадром остались такие важные проблемы, как балансировка деревьев, работа с В-деревь-ями и т. д. После столь обстоятельного введения и наличия соответствующей литературы, вы сможете без особого труда решить эти и другие проблемы. Тем более, что на худой конец любое дерево можно преобразовать в бинарное и работать с ним, используя приемы, описанные в настоящем разделе.

В преддверии рассмотрения следующего материала отметим, что разработанная в этом разделе программа будет очень полезна в процессе построения различных транслирующих программ, частным случаем которых являются компиляторы. Лексикографические деревья можно с успехом использовать в процессе работы сканера, задачей которого, в частности, является выяснение принадлежности некоторого идентификатора к ключевым словам некоторого языка. Введите в файл infile.txt список ключевых слов (разделенных одним пробелом), запустите программу и в памяти вы получите лексикографическое дерево.

Массив

Все истинно великое совершается медленным,

незаметным ростом.

Сенека

Массивы структур — таблицы

Обычной практикой является размещение одинаковых по содержанию экземпляров структур в одном месте, последовательно — друг за другом. В результате образуется логическая структура данных, называемая таблицей. Каждый экземпляр структуры, входящий в таблицу, называется элементом таблицы.

Как физическая структура данных таблица представляет собой линейную последовательность ячеек памяти, число которых определяется количеством и размером полей каждого элемента, а также числом элементов таблицы.

Над таблицей можно определить следующие операции:

включение нового элемента путем расширения таблицы или его вставки на свободное место;

поиск элемента для последующей его обработки;

исключение элемента из таблицы.

Скорость доступа к элементам таблицы при выполнении этих операций зависит от двух факторов — способа организации поиска нужного элемента и размера таблицы.

Механизм работы с кучами Windows

Этот механизм наиболее эффективен для поддержки работы с такими структурами данных, как связные списки, деревья и т. п. Как правило, отдельные элементы этих структур имеют небольшой размер, в то время как общее количество памяти, занимаемое этими структурами в разные моменты времени работы приложения, может быть разным. Главное преимущество использования кучи — свобода в определении размера выделяемой памяти. В то же время это самый медленный механизм динамического выделения памяти.

Windows поддерживает работу с двумя видами куч: стандартной и дополнительной.

Во время создания система выделяет процессу стандартную кучу (или кучу по умолчанию), размер которой составляет 1 Мбайт. При желании можно указать компоновщику ключ /HEAP с новой величиной размера стандартной кучи. Создание и уничтожение стандартной кучи производится системой, поэтому в API не существует функций, управляющих этим процессом. Только одна функция должна вызываться перед началом работы со стандартной кучей — GetProcessHeap:

HANDLE GetProcessHeap(VOID)

GetProcessHeap возвращает описатель, используемый далее другими функциями работы с кучей.

Для более эффективного управления памятью и локализации структур хранения в адресном пространстве процесса можно создавать дополнительные кучи. Сделать это можно с использованием функции HeapCreate:

HANDLE HeapCreate(DWORD flOptions. SIZE_T dwInitialSize, SIZE_T dwMaximutnSize)

Размер создаваемой этой функцией кучи определяется параметрами dwInitialSize (начальный размер) и dwMaximumSize (максимальный размер). Возвращаемое функцией HeapCreate значение — описатель кучи, который используется затем другими функциями, работающими с данной кучей. Уничтожение дополнительной кучи осуществляется вызовом функции HeapDestroy, которой в качестве параметра передается описатель уничтожаемой кучи:

BOOL HeapDestroytHANDLE hHeap)

Важно отметить, что на этапе создания как стандартной, так и дополнительных куч реального выделения памяти для них не производится. Главное — получить указатель и сообщить системе характеристики и размер создаваемой кучи.

После получения описателя работа со стандартной и дополнительной кучами осуществляется с помощью функций НеарАПос, HeapReAlloc, HeapSize, HeapFree. Рассмотрим их подробнее.

Выделение физической памяти из кучи производится по запросу НеарАПос:

LPVOID HeapAlloc(HANDLE hHeap. DWORD dwFlags. SIZEJ dwBytes)

Здесь параметр hHeap сообщает НеарАПос, в пространстве какой кучи требуется выделение памяти размером dwBytes байт. Параметр dwFlags представляет собой флаги, с помощью которых можно влиять на особенности выделяемой памяти. В случае успеха функция НеарАПос возвращает адрес, который используется далее для доступа к физической памяти в выделенном блоке.

В ходе работы с выделенным блоком может сложиться ситуация, когда необходимо изменить его размер в большую или меньшую сторону. Для этого предназначена функция HeapReAHoc:

LPVOID HeapReA11oc(HANDLE hHeap. DWORD dwFlags, LPVOID ipMem, SIZE_T dwByt

Параметр hHeap идентифицирует кучу, в которой изменяется размер блока, а параметр lpMem является адресом блока (полученным ранее с помощью НеарАПос), размер которого изменяется. Новый размер блока указывается параметром dwBytes.

Играя размерами блоков, вы можете совсем запутаться. Функция HeapSize поможет вам определить текущий размер блока по адресу 1 рМет в куче hHeap.

DWORD HeapSize(HANDLE hHeap. DWORD dwFlags, LPCVOIO lpMem)

И наконец, когда блок по адресу lpMem в куче hHeap становится ненужным, его можно освободить вызовом функции HeapFree:

BOOL HeapFreeCHANDLE hHeap. DWORD dwFlags. LPVOID lpMem)

Это минимальный набор функций Windows для работы с кучами. Он столь подробно был обсужден нами с целью дальнейшего использования этих функций для разработки приложений этого раздела.

Механизм виртуальной памяти Windows

Механизм виртуальной памяти Windows реализуется с помощью функций API Win32 VirtualAlloc и VirtualFree.

LPVOID VirtuaUn ос (LPVOID ipAddress. SIZEJ dwSize. DWORD flAllocationType. DWORD

flProtect) BOOL VirtualFreeCLPVOID IpAddress. SIZEJ dwSize, DWORD dwFreeType)

С помощью функции Virtual All ос приложение запрашивает в свое распоряжение область памяти (регион) в адресном пространстве с размером, указываемым параметром dwSize. Величина dwSize должна быть кратна 64 Кбайт, что, соответственно, является минимальным размером региона. Динамическое выделение памяти такими большими порциями может требоваться лишь для работы с большими массивами данных (структурами данных). Для нашего изложения этот способ выделения данных не подходит. Отметим лишь, что работа функции VirtualAlloc имеет следующую особенность. Имеются три варианта обращения к функции VirtualAlloc: резервирование региона в адресном пространстве процесса; выделение физической памяти в зарезервированном предыдущим вызовом функции VirtualAlloc регионе; резервирование региона с одновременной передачей ему физической памяти. Освобождение региона производится функцией VirtualFree. Более подробную информацию о параметрах функций VirtualAlloc и VirtualFree можно посмотреть в MSDN.

Множество

Соня закрыла глаза и задремала. Но тут Болванщик

ее ущипнул, она взвизгнула и проснулась.

—...начинается на М, — продолжала она. — Они

рисовали мышеловки, математику, множество...

Ты когда-нибудь видела, как рисуют множество?

— Множество чего? - спросила Алиса.

— Ничего, — отвечала Соня. — Просто множество!

— Не знаю, — начала Алиса, — может...

— А не знаешь — молчи, — оборвал ее Болванщик.

Льюис Кэрролл. «Алиса в стране чудес»

Множество как структура уровня представления является совокупностью различных объектов, которые могут либо сами являться множествами, либо представлять собой неделимые элементы, называемые атомами.

Множество как структура уровня хранения реализуется двумя способами:

ш простым — в виде данных перечислимого типа; в языках высокого уровня этот тип данных реализуют с помощью типа «множество» (в Pascal) или констант перечислимого типа (в С);

ш сложным — в виде вектора или связного списка.

Отличие этих двух способов в том, что данные перечислимого типа ограниченно поддерживают понятие множества, представляя собой совокупность объектов, которым сопоставлены некоторые значения. При реализации множеств с помощью вектора или связного списка становится возможным реализовать именно математическое понятие множества, согласно которому, над множествами определен ряд операций: объединение, пересечение, разность, слияние, вставка (удаление) элемента и т. д. С данными перечислимого типа эти операции невозможны.

В языке ассемблер также есть средства, позволяющие реализовать оба способа представления множеств. Так, описание данных перечислимого типа поддерживаются с помощью директивы enum. Как и в языках высокого уровня, данные перечислимого типа, вводимые этой директивой, являются константами, которым соответствуют уникальные символические имена. Директива enum имеет следующий синтаксис:

символ_имя enum значение[. значение[, значение....]]

Здесь значение представляет собой конструкцию символ_имя [=число], а символ_ имя — любое символическое имя, не совпадающее с ключевыми словами ассемблера или другими ранее определенными в программе символическими именами. Следующие примеры описания множеств эквивалентны.

week enum Monday.Tuesday,Wednesday,Thursday,Friday,Saturday.Sunday > week enum Monday=0,Tuesday=l. Wednesday^. Thursday=3. Fri day=4.Saturday=5.Sunday=6 week enum Monday=0,Tuesday.Wednesday,Thursday.Fri day.Saturday.Sunday week enum Sunday=6.Monday=0,Tuesday,Wednesday.Thursday,Fri day.Saturday

Перечисление элементов множества может занимать несколько строк в программе.

Транслятор будет отводить под размещение каждого элемента множества столько байтов, сколько требуется для размещения значения самого большого элемента в этом множестве (байт, слово, двойное слово).

Если при описании очередного элемента множества число в некоторой конструкции символ_имя [=число] не задано, то транслятор присвоит этому элементу множества значение, на единицу большее предыдущего. Если ни одного значения не было задано, то первому элементу множества присваивается 0, второму 1 и т. д.

Работа с элементами множества в программе является завуалированной формой использования непосредственного операнда. В этом несложно убедиться, проанализировав листинг трансляции:

5 :задаем множество:

6 =0000 =0001 =0002 + week enum

Monday.Tuesday,Wednesday.Thursday.Fri day.Saturday.Sunday

7 =0003 =0004 =0005 +

8 =0006

20 0005 B8 0006 mov ax,Sunday

Значение символического имени синвол_имя, стоящего слева от директивы enum, равно количеству битов, необходимому для размещения максимального значения элемента справа от директивы enum:

5 ;задаем множество:

6 =0000 =0001 =0002 + week enum

Monday.Tuesday.Wednesday.Thursday,Fri day.Saturday.Sunday

7 =0003 =0004 =0005 +

8 =0006

21 0005 B8 0007 mov ax.week

Перед использованием в программе необходимо определить и инициализировать экземпляр множества:

F_week week Saturday

Размер этой переменной будет соответствовать размеру максимального элемента множества week. Сказанное иллюстрирует фрагмент листинга:

5 :задаем множество:

6 =0000 =0001 =0002 + week enum

Monday.Tuesday,Wednesday.Thursday.Friday.Saturday.Sunday

7 =0003 =0004 =0005 +

8 =0006

9 0000 05 s week Saturday

21 0005 A2 OOOOr movs.al

Хорошо видно, что в данном случае работа с экземпляром множества осуществляется как с байтовой переменной.

Возможности ассемблера для описания множества и работы с ним сложным способом (с помощью векторов и связных списков) будут ясны в ходе дальнейшего изложения.

Неупорядоченный поиск

Для выполнения неупорядоченного (линейного) поиска нет определенных методов. Чтобы эффективно реализовать эту операцию, необходимо умело использовать средства языка программирования. Если поиск ведется в массиве чисел (а не записей с числовым ключевым полем), то наибольшей эффективности для реализации линейного поиска в программе на языке ассемблера можно достичь, если использовать цепочечные команды. Поэтому мы рассмотрим варианты реализации линейного поиска, предполагая, что массив, в котором ведется поиск, на самом деле является массивом записей и использование цепочечных команд не представляется возможным. Для вставки приведенных ниже фрагментов в свои реальные программы вы должны скорректировать соответствующие смещения.

Первый вариант неупорядоченного поиска

Этот вариант программы реализации линейного поиска предполагает обычный перебор до тех пор, пока не будет найден нужный элемент или не будут перебраны все элементы.

ПРОГРАММА prg27_429

//prg27_429 - программа на псевдоязыке линейного поиска в массиве (вариант 1).

//Вход: mas[n] - неупорядоченная последовательность двоичных значений длиной n: k -

искомое значение

//Выход: 1 - позиция в mas[n] (0<i<n-l), соответствующая найденному символу.

ПЕРЕМЕННЫЕ

INT_BYTE n: //длина mas[n]

INTJSYTE mas[n]: //массив для поиска размерностью п (О..п-l)

INTJYTE к; //искомый элемент

INT_W0RD 1-0 //индекс

НАЧ_ПРОГ

s2: ЕСЛИ (k==mas[i]) TO ПЕРЕЙТИ_НА _exit

ЕСЛИ (i=<n) TO ПЕРЕЙТИ_НА s2 _exit: //вывести значение 1 по месту требования КОН_ПРОГ

:prg27_429.asm - программа на ассемблере линейного поиска в массиве (вариант 1).

.data

: задаем массив

mas db 50h.08h.52h.06h.90h.17h,89h.27h.65h.42h.15h.51h.61h.67h.76h.70h

n=$-mas k db 15h

.code

xorsi.si ;1-(s1):=0

mov al ,k s2: cmpal.mas[si] ;ЕСЛИ k==mas[i] TO ПЕРЕЙТИ_НА _exit

je ok

inc si :i :=i+l

cmpsi,n-l :ЕСЛИ i=<n TO ПЕРЕЙТИ_НА s2

jbes2 :реакция на неудачный результат поиска

jmp exit ok: :реакция на удачный результат поиска

Обход узлов дерева

Возможны три варианта обхода дерева:

сверху вниз — корень, левое поддерево, правое поддерево;

слева направо — левое поддерево, корень, правое поддерево;

снизу вверх — левое поддерево, правое поддерево, корень.

Понятно, что процедура обхода рекурсивна. Под термином «обход дерева» понимается то, что в соответствии с одним из определенных выше вариантов посещается каждый узел дерева и с его содержательной частью выполняются некоторые действия. Для нашей задачи подходит только второй вариант, так как только в этом случае порядок посещения узлов будет соответствовать упорядоченному массиву. В качестве полезной работы будем извлекать значение из узла двоичного дерева и выводить его в массив в памяти. Отметим особенности функции LRBeat, производящей обход дерева. Во-первых, она рекурсивная, во-вторых, в ней для хранения адресов узлов используется свой собственный стек. Стек, поддерживаемый на уровне архитектуры микропроцессора, используется для работы процедурного механизма, и мы со своими проблемами только «путаемся у него под ногами».

:prg02_13.asm - программа обхода двоичного дерева поиска (слева направо). ;Вход: произвольный масиив чисел в памяти. :Выход: двоичное дерево в памяти.

объявления структур: nodejxee struc :узел дерева

ends

: для программного стека

desc_stk struc :дескриптор стека

ends

•.описание макрокоманд работы со стеком:

create_stk macro HandHead:REQ.descr:REQ.Si zeStk:=<256>

¦.создание стека

endm

push_stk macro descr:REQ.rg_item:REQ

добавление элемента в стек

endm

pop_stkmacro descr:REQ. rg_item:REQ

извлечение элемента из стека

endm

.data

исходный массив:

masdb 37h.l2h,8h.65h.4h.54h.llh.02h.32h,5h,4h,87h.7h.21h.65h.45h.22h,llh.77h.

51h.26h.73h.35h.12h.49h.37h.52h l_mas=$-mas

упорядоченный массив (результат см. в отладчике): ordered array db 1 mas dup (0)

doubleWord_stkdesc_stk <> -.дескриптор стека

count call dd 0 :счетчик количества рекурсивного вызова процедуры

.code

BuildBinTree proc ;см. prg02_12.asm

:двоичное дерево поиска построено

ret

BuildBinTree endp LRBeat proc

:рекурсивная процедура обхода дерева - слева направо :(левое поддерево, корень, правое поддерево)

inc count_call ;подсчет количества вызовов процедуры

:(для согласования количества записей и извлечений из стека)

cmp ebx.O

je @@exit_p

mov ebx.[ebx].l_son

cmp ebx, 0

je @@ml

push_stk doubleWord_stk.ebx mini: call LRBeat

pop stkdoubleWord stk.ebx

r r_ —

jnc @@m2

:подчистим за собой стек и на выход raovecx.count_call

dec ecx

pop NewNode:pop "в никуда"

loop $-6

jmp @@exi t_p @@m2: moval,[ebx].simbol

stosb

mov ebx, [ebx]. r_son cmp ebx.O je @@ml push stk doubleWord stk.ebx

c'all LRBeat " @@exit_p: deccount_call

ret

LRBeat endp start proc near ;точка входа в программу:

call BuildBinTree :формируем двоичное дерево поиска ;обходим узлы двоичного дерева слева направо и извлекаем значения ;из содержательной части, нам понадобится свой стек (размер (256 байт) нас устроит. :но макроопределение мы подкорректировали)

create_stk Hand_Head.doubieWord_stk

push ds

pop es

lea edi.ordered_array

mov ebx.HeadTree push_stk doubleWord_stk.ebx указатель на корень в наш стек

call LRBeat

Еще одно замечание о рекурсивной процедуре. Реализация рекурсивное™ в программах ассемблера лишена той комфортности, которая характерна для языков высокого уровня. При реализации рекурсивной процедуры LRBeat возникает несбалансированность стека, в результате после последнего ее выполнения на вершине стека лежит не тот адрес и команда RET отрабатывает неверно. Для устранения подобного эффекта нужно вводить корректировочный код, суть которого заключается в следующем. Процедура LRBeat подсчитывает количество обращений к ней и легальных, то есть через команду RET, выходов из нее. При последнем выполнении анализируется счетчик обращений countcal 1 и производится корректировка стека.

Для полноты изложения осталось только показать, как изменится процедур;!. LRBeat для других вариантов обхода дерева.

Построенное выше бинарное дерево теперь можно использовать для дальнейших операций, в частности поиска. Для достижения максимальной эффективности поиска необходимо, чтобы дерево было сбалансированным. Так, дерево считается идеально сбалансированным, если число вершин в его левых и правых поддеревьях отличается не более чем на 1. Более подробные сведения о сбалансированных деревьях вы можете получить, изучая соответствующую литературу. Здесь же будем считать, что сбалансированное дерево уже построено. Разберемся с тем, как производить включение и исключение узлов в подобном, заранее построенном упорядоченном дереве.

Включение узла в упорядоченное бинарное дерево

Задача включения узла в дерево уже была решена нами при построении дерева. Осталось оформить соответствующий фрагмент программы в виде отдельной процедуры addNodeTree. Чтобы не дублировать код, разработаем рекурсивный вариант процедуры включения — addNodeTree. Он хоть и не так нагляден, как нерекурсивный вариант кода в программе prg_03.asm, но выглядит достаточно профессионально. Текст процедуры addNodeTree вынесен на дискету.

Работу процедуры addNodeTree можно проверить с помощью программы prgO2_ 13.asm (в е ей соответствует программа prgO2_14.asm).

В результате проведенных работ мы получили дублирование кода, строящего и дополняющего дерево. В принципе для строительства и включения в дерево достаточно одной процедуры addNodeTree. Но в учебных целях мы ничего изменять не будем, чтобы иметь два варианта строительства дерева — рекурсивный и не рекурсивный. При необходимости читатель сам определит, какой из вариантов более всего отвечает его задаче и в соответствии с этим доработает этот код.

Исключение узла из упорядоченного бинарного дерева

Эта процедура более сложная. Причиной тому то обстоятельство, что существует несколько вариантов расположения исключаемого узла в дереве: узел является листом, узел имеет одного потомка и узел имеет двух потомков. Самый непростой случай — последний. Процедура удаления элемента del NodeTree является рекурсивной и, более того, содержит вложенную процедуру del, которая также является рекурсивной. Текст процедуры del NodeTree вынесен на дискету.

Работу этой процедуры можно проверить с помощью программы prg02_13.asm (в е ей соответствует программа prg02_15.asm).

Графически процесс исключения из дерева выглядит так, как показано на Рисунок 2.20. Исключаемый узел помечен стрелкой.

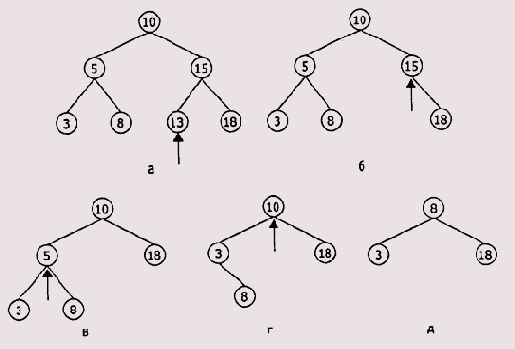
Рисунок 2.20. Исключение из дерева

Для многих прикладных задач, занимающихся обработкой символьной информации, важное значение могут иметь так называемые лексикографические деревья. Для нашего изложения они важны тем, что эффективно могут быть применены при разработке трансляторов, чему мы также уделим внимание в этой книге.

Очередь

Очередь [2, 10, 15] — последовательный список, в котором включение элементов производится на одном конце, а исключение на другом, то есть по принципу FIFO (First In First Out — первым пришел — первым ушел). Сторона очереди, на которой производится включение элементов, называется хвостом. Соответственно, противоположная сторона — голова очереди. Очередь описывается дескриптором, который может содержать поля: имя очереди, адреса верхней и нижней границ области памяти, выделенной для очереди, указатели на голову и хвост. Набор операций для очереди:

создание очереди (create_que);

включение элемента в очередь (push_que);

исключение элемента из очереди (popque);

проверка пустоты очереди (TestEmptyQue);

очистка очереди без освобождения памяти для нее (initque);

удаление очереди (delete_que).

При помощи очереди удобно моделировать некоторые обслуживающие действия, например это может быть некоторая очередь запросов к критическому ресурсу или очереди заданий на обработку. К очереди так же, как и стеку, применимы такие параметры, как емкость очереди и размер элемента очереди.

На практике используются очереди двух типов — простые и кольцевые. Очередь обслуживается двумя указателями — головы (Р,) и хвоста очереди (Р2). Указатель головы Р идентифицирует самый старый элемент очереди, указатель хвоста — первый свободный слот после последнего включенного в очередь элемента. Сами элементы физически по очереди не двигаются. Меняется лишь значение указателей. При включении в очередь новый элемент заносится в ячейку очереди, на которую указывает Р2. Операция исключения подразумевает извлечение элемента из ячейки очереди, указываемой Р,. Кроме извлечения элемента операция исключения производит корректировку указателя Р, так, чтобы он указывал на очередной самый старый элемент очереди. Таким образом, Указатель хвоста простой очереди всегда указывает на свободную ячейку очере-Ди и рано или поздно он выйдет за границы блока, выделенного для очереди. И это случится несмотря на то, что в очереди могут быть свободные ячейки

( ячейки А. Чтобы исключить это явление, очередь организуется по принципу кольца. В обоих способах организации очереди важно правильно определить ее емкость. Недостаточный объем очереди может привести в определенный момент к ее переполнению, что чревато потерей новых элементов, претендующих на включение в очередь.

Для иллюстрации порядка организации и работы с очередью рассмотрим пример. Пусть имеется строка символов, которая следующим образом моделирует некоторую вычислительную ситуацию: символы букв означают запросы на некоторый ресурс и подлежат постановке в очередь (имеющую ограниченный размер). Если среди символов встречаются символы цифр в диапазоне 1-9, то это означает, что необходимо изъять из очереди соответствующее значению цифры количество элементов. Если очередь полна, а символов цифр все нет, то происходит потеря заявок (символов букв). В нашей программе будем считать, что очередь кольцевая и ее переполнение помимо потери новых элементов приводит к выводу соответствующего сообщения. Для кольцевой очереди возможны следующие соотношения значений указателей Р, и Р2: Pj < Р2, Pj = Р2 (пустая очередь), Р, > Р2. Память для очереди в нашей задаче выделяется динамически средствами API Win32.

Заметим, что исходя из потребностей конкретной задачи можно изменить дисциплину обслуживания очереди. Например, установить, что при переполнении очереди потере подлежат старые заявки (в голове очереди) и т. п.

jb ml cmpa1.39h

ja ml

xor есх.есх:удгляем из очереди элементы

mov cl,al

subcl,30h преобразуем символ цифры в двоичный эквивалент ш2: pop_quechar_que.<offset temp>

jc cycl ;если очередь пуста

1 oop m2

jmpcycl ml: добавляем элементы в очередь

mov temp,a 1

push_que char_que. <offset temp>

jnc cycl ;ycnex ;вывод на экран сообщения об ошибке - отсутствие места в очереди

jmp cycl

;выход из приложения exit: :удаляем блок памяти с очередью

delete_que char_que

Как и в случае со стеком, код, выполняющий работу с очередью, оформлен в виде макрокоманд. Программа выдает единственное Сообщение о переполнении очереди. Чтобы наблюдать работу программы в динамике, необходимо выполнить следующие действия.

1. Загрузить исполняемый модуль программы в отладчик td32.exe.

2. Отследить адрес начала блока памяти, который будет выделен системой по нашему запросу для размещения очереди. Для этого подвергните пошаговому выполнению в окне CPU содержимое макрокоманды createque.

3. Выяснив адрес начала блока для размещения очереди, отобразите его в окне Dump и нажмите клавишу F7 или F8. Не отпуская этой клавиши, наблюдайте за тем, как изменяется состояние очереди.

Односвязные списки

В простейшем случае односвязный список можно организовать в виде двух одномерных массивов, длины которых совпадают и определяются максимально возможной длиной списка. Поля первого массива содержат собственно данные, а соответствующие поля второго массива представляют собой указатели. Значением каждого из этих указателей является индекс элемента первого массива, который логически следует за данным элементом, образуя таким образом связанный список. В качестве примера рассмотрим программу, которая в некотором массиве связывает все ненулевые элементы, а затем в качестве полезной работы подсчитывает их количество. В последний единичный элемент в качестве признака конца списка заносим Offh.

:prg3_10.asm - пример реализации односвязных списков с помощью двух массивов

:Вход: массивы с данными и указателями.

:Выход: нет. В динамике работа программы наблюдается под управлением отладчика.

.data

masdb 0.55.0.12.0.42.94.0.18.0.06.67.0.58.46 :задаем массив

n=$-mas

point db 0 указатель списка - индекс первого ненулевого элемента в mas

masjraint db n dup (0) определим массив указателей

.code

lea si.mas :b si адрес mas_point

xorbx.bx :b bx будут индексы - кандидаты на включение в массив указателей :ищем первый ненулевой элемент

movcx,n-l cycll: cmpbyte ptr [si][bx].O

jneml :если нулевые элементы

inc bx

loop cycll

jmpexit ;если нет ненулевых элементов ml: mov point.Ы :запоминаем индекс первого ненулевого в point

movdi.bx ;в di индекс предыдущего ненулевого ;просматриваем далее (сх тот же)

inc bx сус12: cmpbyte ptr [si][bx].O

je m2 ;нулевой => пропускаем :формируем индекс

movmas_point[di].bl ;индекс следующего ненулевого в элемент mas_point предыдущего

movdi.bx :запоминаем индекс ненулевого

т2: inc bx

loop cycl2

mov mas_point[di].Offh ;индекс следующего ненулевого в элемент mas_point ;выход :а теперь подсчитаем единичные, не просматривая все. - результат в ах

хог ах.ах

cmp point.0

je exit,

inc ax

mov bl .point cycl3: cmp mas_point[bx].Offh

je exit

inc ax

mov Ы ,mas_point[bx]

jmpcycl3 результат подсчета в ах. с ним нужно что- то делать, иначе он будет испорчен

Если количество нулевых элементов велико, то можно сократить объем хранения данного одномерного массива в памяти (см. ниже материал о разреженных массивах).

Кстати, в качестве еще одного реального примера использования односвязных списков вспомните, как реализован учет распределения дискового пространства в файловой системе MS DOS (FAT).

Далее рассмотрим другой, более естественный вариант организации связанного списка. Его элементы содержат как содержательную, так и связующую части.

Рассуждения относительно содержательной части пока опустим — они напрямую зависят от конкретной задачи. Уделим внимание связующей части. Понятно, что это адреса. Но какие? Можно считать, что существуют два типа адресов, которые могут находиться в связующей части: абсолютные и относительные. Абсолютный адрес в конкретном элементе списка — это, по сути, смещение данного элемента относительно начала сегмента данных или блока данных при динамическом выделении памяти и принципиально он лишь логически связан со списком. Относительный адрес формируется исходя из внутренней нумерации элементов в списке и имеет смысл лишь в контексте работы с ним. Пример относительной нумерации рассмотрен выше при организации списка с помощью двух массивов. Поэтому далее этот способ адресации мы рассматривать не будем, а сосредоточимся на абсолютной адресации.

Для начала разработаем код, реализующий применительно к односвязным спискам основные из обозначенных нами выше операций со связанными списками. Односвязные списки часто формируют с головы, то есть включение новых элементов производится в голову списка.

Первая проблема — выделение памяти для списка. Это можно делать либо статическим способом, зарезервировав место в сегменте данных, либо динамически, то есть так, как мы это делали выше при реализации операций со стеками и очередями. Недостатки первого способа очевидны, хотя в реализации он очень прост. Гораздо интереснее и предпочтительнее второй способ, который предполагает использование кучи для хранения связанного списка. Для придания боль-Шей реалистичности изложению рассмотрим простую задачу: ввести с клавиатуры

символьную строку, ограниченную символом "." (точка), и распечатать ее в обратном порядке.

:prgl5_102.asm - реализация программы инвертирования строки с односвязными списками

:Вход: символьная строка с клавиатуры.

:Выход: вывод на экран инвертированной обратной строки.

;.........

itemjist struc :элемент списка

next dd 0 :адрес следующего элемента

info db 0 содержательная часть (в нашем случае - символ)

ends

.data

mas db 80 dup С ') :в эту строку вводим

mas revdb 80 dup (' ') :из этой строки выводим

len mas rev=$-mas rev

mesl db 'Введите строку символов (до 80) для инвертирования (с точкой на конце):'

len_mesl=$-mesl

.code

списание макрокоманд работы со связанным списком;

createjist macro descr:REQ.head:REQ

: создание списка - формирование головы списка и первого элемента

;.........

endm

addjist macro descr:REQ.head:REQ.H_Head:REQ

добавление элемента в связанный список

endm

createjtem macro descr:REQ.H_Head:REQ

;создание элемента в куче для последующего добавления в связанный список

¦.........

endm

start proc near :точка входа в программу:

:вывод строки текста - приглашения на ввод строки для инвертирования !.........

:вводим строку в mas

:.........

;создаем связанный список createjist itemJist.HeadJist :первый элемент обрабатываем отдельно

leaesi.mas

moval.[esi]

cmp al."."

je rev_out

mov [ebx].info.al

:вводим остальные символы строки с клавиатуры до тех пор. пока не встретится "." cycl: incesi

mov al.[esi]

cmp al,"."

je rev_out

addj i st i temj i st. HeadJ i st. Hand_Head

mov [ebx].info.al

jmp cycl

:вывод строки в обратном порядке rev_out: mov esi.offset mas_rev

mov ebx,HeadJist cycl2: mov al .[ebx].info

mov [esil.al

inc esi

mov ebx.[ebx].next

cmpebx.Offffffffh

jne cycl2 ; выводим инвертированную строку на экран

Недостаток такого способа построения списка — в порядке включения элементов. Хорошо видно, что он обратный порядку поступления элементов. Для исправления данной ситуации можно, конечно, ввести еще один указатель на последний элемент списка. Есть и другой вариант — организация двусвязного списка. Уделим теперь внимание другим операциям с односвязным списком.

Включение в список

Для включения нового элемента в список необходимо предварительно локализовать элемент, до или после которого будет производиться это включение. Для того чтобы включить новый элемент после локализованного, необходимо выполнить действия, отраженные фрагментом кода:

itemjist struc элемент списка

next dd 0 ; адрес следующего элемента

info db 0 содержательная часть (в нашем случае - символ)

предполагаем, что адрес локализованного элемента находится в регистре ЕВХ.

:а адрес нового элемента - в ЕАХ

mov edx.[ebx].next

mov [eax].next.edx mov [ebx].next.eax

Для включения нового элемента после локализованного возникает проблема, I источник которой в однонаправленности односвязного списка, так как, по определению, проход к предшествующему элементу невозможен. Можно, конечно, включить новый элемент, как показано выше, а затем попросту обменять содержимое этих элементов. К примеру, это может выглядеть так:

itemjist struc :элемент списка

next dd 0 :адрес следующего элемента

info db 0 содержательная часть (в нашем случае - символ)

ends

предполагаем, что адрес локализованного элемента находится в регистре ЕВХ.

:а адрес нового элемента - в ЕАХ

mov edx.[ebx].next mov [eax].next.edx mov edx.[ebx].info mov [eax].info.edx mov [ebx].next.eax

:осталось заполнить поле info нового элемента

Но если производится включение в упорядоченный список, то логичнее работать с двумя указателями — на текущий и предыдущий элементы списка, так как это показано ниже. При этом предполагается, что новый элемент создается описанной в предыдущей программе макрокомандой create_item.

описание элемента списка

item_list struc :элемент списка

next dd 0 ; адрес следующего элемента

info db 0 содержательная часть (в нашем случае - символ)

ends

.data

ins_itern itemjist <.15> вставляемый элемент (поле info содержит значение -

:критерий вставки)

Headjist dd Offffffffh указатель на начало списка (Offffffffh - список пуст) Hand_Head dd 0 ;переменная, в которой хранится дескриптор кучи

.code

;здесь мы инициализировали и работали со списком

;список упорядочен по возрастанию

:ищем место вставки

;1 - выбираем первую ячейку

mov ebx.HeadJist .

хогеах.еах ; в еах будет указатель на предыдущий элемент ;2 последняя ячейка? ml: cmpebx.Offffffffh

je noJtern :список пустой :3 - новая ячейка до очередной выбранной? ovd1.CebxJ.info cmpdl.ins_item.info ja nextjtem cmpeax. jne into ;вставить первым

createjtem i temj i st. H_Head :макрос создания элемента в куче mov Headjist.edx :адрес нового в голову списка

mov [edx].next.ebx ;настройка указателей jmpexit :на выход

вставить внутрь списка

into: createjtem item_list.H_Head :макрос создания элемента в куче mov [еах].next.edx :адрес нового в поле next предыдущего mov [edx].next.ebx :в поле next нового адрес текущего jmp exit :на выход

: выбор очередного элемента nextjtem: moveax.ebx:aflpec текущего в еах mov ebx. [ebx].next jmp ml

:4 - список пуст или нет больше элементов no J tern: cmpeax.O

jne no_empty :список непустой :список пуст

mov Headjlist.edx :адрес нового в голову списка

mov [edx].next.Offffffffh:это будет пока единственный элемент в списке

jmpexit :на выход

no_empty: :список не пуст - новая ячейка в конец списка

mov [еах].next.edx

mov [edx].next.Offffffffh:это будет последний элемент в списке

exit: :общий выход

Исключение из списка

Алгоритм предполагает наличие двух указателей — на текущую и предыдущую ячейки. Для разнообразия этот алгоритм предполагает прямой порядок следования элементов в списке. В качестве упражнения читателю предлагается, если нужно, переписать приводимый ниже фрагмент для обратного порядка следования элементов.

:описание элемента списка

itemjist struc -.элемент списка

next dd 0 :адрес следующего элемента

info db 0 содержательная часть (в нашем случае - символ)

ends

.data

search_b db 0 критерий поиска (поле info экземпляра структуры itemjist)

Headjist dd Offffffffh указатель на начало списка (Offffffffh - список пуст)

.code

:здесь мы инициализировали и работали со списком

:ищеи ячейку, подлежащую удалению ;1 - выбираем первую ячейку

mov ebx.HeadJist

хогеах,еах; в еах будет указатель на предыдущую ячейку ;2 последняя ячейка?

cmpebx.Offffffffh

je no J tem cycl: cmp [ebx].info.search_b сравниваем с критерием поиска

jnechjiextjtem : нашли? ;да. нашли!

cmpeax.

jne no_fist:зто не первая ячейка :первая ячейка (?) »> изменяем указатель на начало списка и на выход

mov edx.[ebx].next

mov Headjist.edx

jmpexit no_fist: mov [eax].next.ebx перенастраиваем указатели -> элемент удален

jmpexit ;на выход

:выбор следующего элемента ch_nextjtem; mov eax.ebx : запомним адрес текущей ячейки в указателе на предыдущую

mov ebx.[ebx].next ;адрес следующего элемента в ebx

jmp cycl

:обработка ситуации отсутствия элемента nojtem:

Остальные обозначенные нами выше операции очевидны и не должны вызвать у читателя трудностей в реализации.

Другой интересный и полезный пример использования односвязных списков — работа с разреженными массивами. Разреженные массивы представляют собой массивы, у которых много нулевых элементов. Представить разреженный массив можно двумя способами: с использованием циклических списков с двумя полями связи и с использованием хэш-таблицы.

С разреженными массивами можно работать, используя методы хэширования. Для начала нужно определиться с максимальным размером хэш-таблицы М для хранения разреженного массива. Это значение будет зависеть от максимально возможного количества ненулевых элементов. Ключом для доступа к элементу хэш-таблицы выступает пара индексов (i,j), где i = l..p, j = l..q. Числовое значение ключа вычисляется по одной из следующих формул

Остальные действия зависят от избранного способа вычисления хэш-функции (см. выше соответствующий раздел о методах хэширования).

Описание массивов

Как структура представления массив является упорядоченным множеством элементов определенного типа. Упорядоченность массива определяется набором целых чисел, называемых индексами, которые связываются с каждым элементом массива и однозначно определяют его расположение среди других элементов массива. Локализация конкретного элемента массива — ключевая задача при разработке любых алгоритмов, работающих с массивами. Ее сложность прямо зависит от размерности массива.

Наиболее просто представляются одномерные массивы. Соответствующая им структура хранения — это вектор. Она однозначна и представляет собой просто последовательное расположение элементов в памяти. Чтобы локализовать нужный элемент одномерного массива, достаточно знать его индекс. Так как ассемблер не имеет средств для работы с массивом как структурой данных, то для использования элемента массива необходимо вычислить его адрес. Для вычисления адреса i-ro элемента одномерного массива можно использовать формулу:

Аi=АБ+i*lеn

Здесь АБ — адрес первого элемента массива размерностью n, i — индекс (i=0.. n-1), len — размер элемента массива в байтах. Заметьте, что при таком определении можно не говорить о типе элементов массива. В общем случае они также могут быть структурированными объектами данных.

Представление двумерных массивов немного сложнее. Здесь мы имеем случай, когда структуры хранения и представления различны. О структуре представления говорить излишне — это матрица. Структура хранения остается прежней — вектор. Но теперь его нельзя без специальных оговорок интерпретировать однозначно. Все зависит от того, как решил разработчик программы «вытянуть» массив — по строкам или по столбцам. Наиболее естествен порядок расположения элементов массива — по строкам. При этом наиболее быстро изменяется последний элемент индекса. К примеру, рассмотрим представление на логическом уровне двумерного массива Ац размерностью nxm, где 0 < i < n—I, 0 < j < m-1:

а00 а01 а02 а03

а10 а11 а12 а13

а20 а21 а22 а23

а30 а31 а32 а33
Соответствующее этому массиву физическое представление в памяти — вектор — будет выглядеть так:
а00 а01 а02 а03а10 а11 а12 а13а20 а21 а22 а23а30 а31 а32 а33
Номер конкретного элемента массива в этой, уже как бы ставшей линейной, последовательности определяется адресной функцией, которая устанавливает положение (адрес) в памяти этого элемента исходя из значения его индексов:
aij=n*i + j.
Для получения адреса элемента массива в памяти необходимо полученное значение умножить на размер элемента и сложить с базовым адресом массива.

Аналогично осуществляется локализация элементов в массивах большей размерности. На Рисунок 2.1 показан трехмерный массив Aijz размерностью n x m x к, где n = 4, m = 4, к = 2.

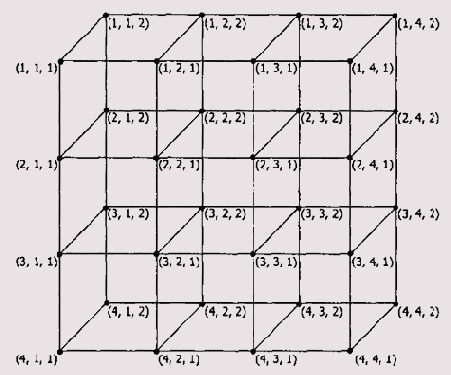
Рисунок 2.1. Пример логической структуры трехмерного массива
Cоответствующий этому массиву вектор памяти будет выглядеть так:а120
а000 а001 а010а011а020 а021 а030 а031а100 а101 а111 а120.. а331

Соответственно номер элемента определяется так:
aijz=n*m*i + m*j + z, где 0 < i < n-1, 0 < j < m-1, 0 < z < k-1.
Для получения адреса осталось умножить полученное значение на размер элемента массива и сложить результат с базовым адресом массива.

Таким образом, преобразование многомерной, в общем случае логической структуры массива в одномерную физическую структуру производится путем ее линеаризации по строкам или столбцам. В первом случае, быстрее всего изменяется последний индекс каждого элемента, во втором — первый индекс. Недостаток описанного способа локализации элемента массива в том, что процесс вычисления адреса подразумевает выполнение операций сложения и умножения. Как известно, они не являются быстрыми. Существует метод Дж. Айлиффа, с помощью которого можно исключить операцию умножения из процесса вычисления индекса. Индексация в массиве производится с помощью иерархии дескрипторов, называемых векторами Айлиффа, так как это показано на Рисунок 2.2. На этом рисунке j,, )ь j3 обозначают соответственно первый, второй и третий индексы массива.

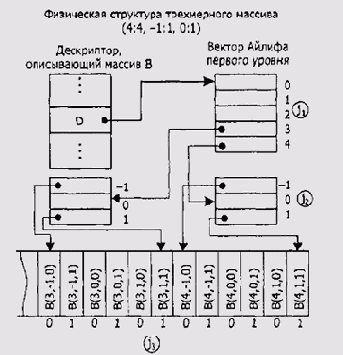
Рисунок 2.2. Представление предыдущего трехмерного массива по методу Айлиффа
Из рисунка видно, что основной дескриптор массива содержит указатель на вектор Айлиффа первого уровня. Вектор первого уровня является единственным и содержит указатели векторов Айлиффа следующего уровня. То есть, иерархия дескрипторов однозначно отражает размерность массива. Локализовать нужный элемент массива можно, руководствуясь его индексом логического уровня. Для этого нужно пройти по цепочке от основного дескриптора через соответствующие элементы векторов Айлиффа, извлекая из них и суммируя значения смещений с базовым адресом массива:

Здесь (D) — значение указателя вектора Айлиффа первого уровня, хранящееся в основном дескрипторе. При необходимости никто не мешает вам разместить в элементах векторов Айлиффа и другую служебную информацию, например диапазон изменения соответствующего индекса. Очевидный недостаток метода Айлиффа — увеличение общего объема памяти для структуры хранения многомерного массива в памяти.

Что касается описания массива в программе на ассемблере, то его варианты были подробно рассмотрены в учебнике. Перечислим их очень конспективно:
перечисление элементов массива в поле операндов одной из директив описания данных;
резервирование памяти для элементов массива с использованием оператора повторения dup (элементы массива формируются динамически в ходе выполнения программы);
использование директив label и rept.
После рассмотрения возможностей по динамическому выделению памяти в операционных средах MS DOS и Windows можно к перечисленным трем вариантам добавить еще один — динамическое распределение памяти. Применительно к программированию для Windows возможности здесь очень широкие и можно использовать наиболее подходящий способ из трех, обсуждавшихся в разделе «Способы распределения памяти».

Массив в разное время работы с ним может изменять свои характеристики — имя массива, адрес в памяти первого его элемента, количество и диапазон изменения индексов, тип элементов, размерность и т. п. В этом случае имеет смысл его физическое представление в памяти предварять специальным заголовком, или дескриптором, в котором указывать характеристики массива, чтобы программа могла правильно обрабатывать элементы массива. Особенно это важно, когда память для массива выделяется динамически.

Описание процесса трансляции программы

Транслятор представляет собой программу, выполняющую анализ исходного кода на некотором языке программирования и формирующую объектный модуль. Процесс преобразования исходного кода называется трансляцией. Вместо термина «транслятор», часто употребляется слово «компилятор», и соответственно процесс преобразования называется компиляцией. Не вдаваясь в описание лишних подробностей, будем считать эти названия синонимами и в дальнейшем изложении использовать их исходя из своих пристрастий.

Для многих транслятор представляется как некий черный ящик, которому программист много раз на день доверяет выстраданную им программу. При общении программиста с транслятором возможны два варианта исхода: удачный, при котором на выходе транслятора формируется объектный модуль, и неудачный, когда транслятор обнаруживает в программе различные ошибки. Давайте заглянем в черный ящик, именуемый транслятором, и посмотрим, каким образом он работает. Конечно же, нашему взгляду будут доступны только общие принципы его функционирования, но мы их рассмотрим с той степенью детализации, чтобы можно было самим разработать нечто подобное.

Трансляция программы производится в несколько этапов.

1. Лексический анализ.

2. Синтаксический анализ.

3. Генерация кода.

На каждом из этих этапов выполняется вполне определенная работа. В общем случае проблема компиляции заключается в поиске соответствия написанных программистом предложений структурам, определенным грамматикой, и генерации соответствующего кода для каждого предложения.

Итак, файл исходной программы подготовлен, после чего мы некоторым образом передаем его транслятору для обработки. Происходить это может двумя способами: посредством командной строки (возможно, с использованием утилиты make.exe) либо в интегрированной среде. По сути, для транслятора оба эти способа одинаковы, так как ядро транслятора для обработки этих файлов будет одно. Единственное отличие в том, что в первом случае программист явно формирует все необходимые ключи и параметры командной строки, а во втором случае он это делает неявно, путем настройки параметров интегрированной среды.

Основные понятия

Процесс разработки программы на ассемблере традиционно осложняется тем, что в этом языке ограничены средства описания данных, привычные для языков программирования высокого уровня. В уроке 12 «Сложные структуры данных» учебника были рассмотрены средства, которые поддерживает ассемблер для работы с данными. Но это деление весьма условно и не дает представления о том, как реализуется общая концепция понятий «данное», «тип данных» и «структура данных» в контексте программирования на языке ассемблера. Это обстоятельство существенно влияет на эффективность изучения и использования языка ассемблера. Учитывая сложность и практическую важность данного вопроса, есть смысл изложить его более систематично.

Проблема представления и организации эффективной работы с данными возникла одновременно с идеей разработки первой вычислительной машины. Вычислительная машина функционирует согласно некоторому алгоритму. А если есть алгоритм, то должны быть и данные, с которыми он работает. Аналогично извечной дилемме о курице или яйце возникает вопрос о первичности алгоритма и данных. Схожий вопрос неявно заложен в название небезызвестной книги Никлауса Вирта — «Алгоритмы + структуры данных = программы», два издания которой были выпущены издательством «Мир» в 1985 и 1989 годах.

Что же представляют собой понятия «данное», «тип данного», «структура данных»? Попытаемся привести некую классификационную характеристику этих понятий.

Данное — набор байт, рассматриваемый безотносительно к заложенному в них смыслу. Понятие «обработка данных» характерно для процессора как исполнительного устройства. При этом «данное» рассматривается как совокупность двоичных разрядов, которыми манипулирует определенная машинная команда. Для человека подобную интерпретацию вряд ли можно считать удобной. Для него более естественной является логическая интерпретация данных, которая базируется на понятии «типа данных».

Тип данных можно определить множеством значений данного и набором операций над этими значениями. В учебнике с точки зрения типа данные были разделены на две группы — простые и сложные. Данными простого типа считаются элементарные, неструктурированные данные, которые могут быть описаны с помощью одной из директив резервирования и инициализации памяти. Примером таких данных являются целые и вещественные числа различной размерности. В языках высокого уровня в качестве простых данных используются еще и данные символьного, логического, указательного типов. Данные простого типа называют упорядоченными (или скалярными), так как теоретически можно перечислить все значения, которые они могут принять.

Отличительная особенность данных простого типа — их неструктурированность. В контексте конкретной задачи исходя из смысла и логики обработки между некоторыми простыми данными могут существовать определенные отношения И связи, что позволяет рассматривать их как определенным образом организованные совокупности. Обобщенное название таких совокупностей — структуры данных. В общем случае отдельная структура данных может содержать не только простые данные, но и другие структуры данных.

С известной долей условности можно сказать, что тип данного и структура данных — понятия, не зависимые от компьютерной платформы. Вполне можно абстрагироваться от представления в программе данных простого или сложного типа и проводить теоретические рассуждения относительно действий с целыми и вещественными числами, массивами, списками, деревьями и т. д. Поэтому такие структуры данных называют структурами данных уровня представления, абстрактными, или логическими, структурами. Для машинной обработки абстрактные типы и структуры данных необходимо некоторым способом представить в оперативной памяти, то есть в виде физической структуры данных {структуры хранения), которая, в свою очередь, отражает способ физического представления абстрактных данных на конкретной программно-аппаратной платформе. В качестве примера можно привести двумерный массив. Для программиста, пишущего программу для обработки этого массива, он видится в виде матрицы, содержащей определенное количество строк и столбцов. В оперативной памяти данный массив представляется в виде линейной последовательности ячеек. В данном случае логическая структура данных — двумерный массив, а соответствующая ему физическая структура — вектор (см. ниже). Таким образом, в большинстве случаев существует различие между логическими и соответствующими им физическими структурами данных. Задачей программиста фактически является написание кода, осуществляющего отображение логической структуры на физическую и наоборот. Этот код реализует различные операции логического уровня над структурой данных. Так, на логическом уровне доступ к элементу двумерного массива осуществляется указанием номеров столбца и строки в матрице, в которой расположен данный элемент. На физическом уровне эта операция выглядит по-другому. Для доступа^ к определенному элементу массива программный код по известному номеру строки и столбца вычисляет смещение от начального адреса массива в памяти. Исходя из вышеприведенных рассуждений конкретную структуру данных можно характеризовать ее логическим (абстрактным) и физическим (конкретным) представлениями, а также совокупностью операций на этих уровнях.

Язык ассемблера — язык уровня архитектуры конкретного компьютера. Память компьютеров с архитектурой Intel представляет собой упорядоченный набор непосредственно адресуемых машинных ячеек (байтов). Исходя из этого номенклатура структур хранения данных архитектурно ограничена следующим набором: скаляр, вектор, список, сеть.

Скаляр — поле, содержащее одиночное двоичное значение, размерностью один или несколько байтов. Количество байтов, составляющих скаляр, определяется допустимыми размерами операндов системы команд конкретного процессора.

Вектор — конечное упорядоченное множество расположенных рядом скаляров одного типа, называемых элементами вектора. По сути дела вектор — это одномерный массив. Что у них общего? Геометрически вектор представляет собой состоящий из точек объект в пространстве, имеющий начальную точку, из которой он выходит, и конечную точку, в которую он приходит. Точки, лежащие в пространстве между начальной и конечной точками (элементы вектора), находятся между собой в единственно возможном отношении — отношении непосредственного следования. Такая строгая упорядоченность элементов вектора позволяет произвести их последовательную нумерацию. Аналогично и одномерный массив имеет началом и концом скаляры, расположенные по определенным адресам памяти. Между этими адресами последовательно расположены скаляры, составляющие элементы массива. Определенность с начальным и конечным адресами массива, а также с размерностью его элементов дает возможность однозначно идентифицировать любой его элемент.

Список — набор элементов, каждый из которых состоит из двух полей. Одно поле содержит элемент данных или указатель на элемент данных, другое -указатель на следующий элемент списка, который, в свою очередь, тоже может быть начальным или промежуточным элементом другого списка. Наличие явного указания на упорядоченность элементов списка позволяет достаточно легко манипулировать содержимым списка, включая новые и исключая старые элементы списка без их фактического перемещения в памяти. Это свойство позволяет размещать в памяти динамически изменяющиеся структуры данных.

Сеть — набор элементов, каждый из которых помимо информационного поля содержит несколько полей-указателей на другие элементы сети. С помощью сети удобно представлять такие структуры данных уровня представления, как деревья, ориентированные графы и т. п.

Как мы увидим ниже, эти четыре структуры хранения дают возможность представить в памяти машины практически все известные структуры уровня представления: массивы, записи, таблицы, стеки, Точереди, деки, списки различной степени связности, деревья, ориентированные и неориентированные графы. Эти структуры можно классифицировать по следующим признакам.

Связность, то есть отсутствие или наличие явно заданных связей между элементами структуры. К несвязным структурам уровня представления относятся массивы, символьные строки, стеки, очереди. К связным структурам уровня представления относятся связные списки.

Изменчивость, то есть изменение числа элементов и (или) связей между элементами структуры. По этому признаку структуры делятся на статические (массивы, таблицы), полу статические (стеки, очереди, деки) и динамические (одно-, двух- и многосвязные списки).

Упорядоченность — линейные (массивы, символьные строки, стеки, очереди, одно- и двусвязные списки) и нелинейные (многосвязные списки, древовидные и графовые структуры).

Отображение структур представления в структуры хранения производится в соответствии с требованиями конкретной задачи и в зависимости от требований последней может производиться разными способами. В ходе дальнейшего изложения мы выясним возможности, которыми обладает язык ассемблера для представления и программной обработки наиболее полезных и часто используемых на практике структур представления (абстрактных типов данных).

Поиск в массивах

Поиск информации является одной из самых распространенных проблем, с которыми сталкивается программист в процессе написания программы. Правильное решение задачи поиска для каждого конкретного случая позволяет значительно повысить эффективность исполнения программы. Для общего случая обычно предполагается, что поиск ведется среди массива записей определенной структуры. В каждой записи есть уникальное ключевое поле. Абстрагируясь, можно сказать, что массив записей — это массив ключевых полей. В этом случае задачу поиска в массиве записей можно свести к задаче поиска в массиве ключевых слов. В этом разделе мы обсудим проблему поиска в массивах и пути ее решения. В отличие от методов сортировки классификация методов поиска не отличается особым разнообразием. Уверенно можно сказать, что методы поиска будут различными для упорядоченных и неупорядоченных массивов. Неупорядоченными массивами здесь считаются массивы, о порядке следования элементов которых нельзя сделать никаких предположений. Для таких массивов особых способов поиска нет, кроме как последовательно просматривать все их элементы. В теории такой поиск называется линейным. Если элементы массивов каким-то образом отсортированы, то речь идет об упорядоченных массивах и для поиска в них существует определенный набор методов. В следующих разделах мы рассмотрим ассемблерную реализацию наиболее интересных методов поиска, применяемых в тех случаях, когда ключевое поле — некоторое число. Большой интерес представляют методы поиска в строке, которые рассматриваются в главе 4. И наконец, существует третий класс методов поиска, основанный на арифметическом преобразовании исходных ключей — «хэшировании». Эти методы мы рассмотрим в разделе «Поиск в таблице».

Поиск в таблице

Перечисленные выше операции с таблицей предполагают, что для однозначного доступа к ее элементам последние должны содержать один или более признаков, отличающих их от других элементов этой таблицы. С этой целью в логическую структуру элемента включается по крайней мере одно поле — ключ, содержимое которого уникально для любого из элементов, входящих в таблицу. В общем случае работа с таблицами сводится к методам решения задачи поиска нужного элемента таблицы по заданному значению ключа. Результат решения — получение адреса искомого элемента или заключение о его отсутствии. Для локализации элемента таблицы необходимо знать два адресных компонента — адрес таблицы и смещение нужного элемента относительно начала таблицы. Адрес таблицы получить несложно, так как он является адресом ее первого элемента. Что же касается определения второй компоненты адреса, то для этого существует ряд методов, рассмотрению которых и будет посвящено дальнейшее изложение.

В ряде случаев наряду с ключевым полем определяют еще одно служебное поле — поле текущего состояния элемента, которое может принимать три значения:

элемент свободен — после инициализации таблицы элемент ни разу не использовался для хранения полезной информации;

элемент используется для хранения полезной информации;

элемент удален — после инициализации таблицы элемент хотя бы один раз использовался для хранения полезной информации, после чего был освобожден.

Целесообразность использования поля текущего состояния элемента будет видна из дальнейших рассуждений.

С точки зрения организации поиска таблицы делятся на:

неупорядоченные;

древовидные;

упорядоченные;

с вычисляемыми входами (хэш-таблицы).

Неупорядоченные таблицы

Это простейший вид организации таблиц. Элементы располагаются непосредственно друг за другом, без пропусков. Процесс поиска нужного элемента выполняется очень просто — последовательным перебором элементов таблицы начиная с первого. При этом анализируется ключевое поле и в случае удовлетворения его условию поиска нужный элемент локализуется. Такой способ поиска называется последовательным, или линейным. Для добавления нового элемента необходимо найти первое свободное место, после чего выполнить операцию добавления. Процесс удаления можно реализовать следующим образом. После локализации нужного элемента его поле текущего состояния необходимо установить в состояние «элемент удален». Тогда процесс поиска места для добавления нового элемента будет заключаться в поиске такого элемента, у которого поле текущего состояния элемента имеет значение «элемент удален» или «элемент свободен». Можно еще более оптимизировать работу с неупорядоченной таблицей путем введения в начале таблицы (или перед ней) дескриптора, поля которого содержали бы информацию о размере таблицы, положении первого свободного элемента и т. д.

Обычно неупорядоченные таблицы используют в качестве временных для хранения небольшого количества элементов (до 20). Для таблиц большего размера такая организация поиска неэффективна, поэтому для них следует применять другие способы локализации нужного элемента.

Приемы работы с неупорядоченной таблицей продемонстрируем на примере следующей задачи. Необходимо прочитать содержимое файла maket.txt и обо всех десятичных и шестнадцатеричных числовых константах собрать информацию о значении константы и номере строки, в которой данная константа встретилась. Вывести информацию о десятичных константах на экран. Для того чтобы избежать возни с несущественными деталями, введем следующие ограничения:

содержимое файла — идентификаторы и константы, разделенные не более чем одним пробелом, перед первым или последним идентификатором или константой в строке также следуют по одному пробелу;

для удобства преобразования предполагаем, что длина и количество строк файла maket.txt находятся в диапазоне 0..99, а общая длина файла — не более 240 байт.

Поле текущего состояния представляет собой запись, битовые поля которой означают следующее:

биты 0 и 1 — состояние элемента: 00 — свободен; 01 — используется; 10 — удален;

бит 2 — тип константы: 0 — десятичная константа; 1 — шестнадцатеричная константа;

бит 3 — 0 — не последний элемент таблицы; 1 — последний элемент таблицы.

:prg02_05.asm - программа на ассемблере демонстрации работы с неупорядоченной таблицей ;Вход: файл maket.txt с идентификаторами, среди которых присутствуют десятичные

и шестнадцатеричные константы. ;Выход: вывод информации о десятичных константах на экран.

state_tab struc

last_off dw 0 ;адрес первого байта за концом таблицы

elem_free dw 0 ;адрес первого свободного элемента (Offffh - все занято)

ends

constant struc

state db 0 ;поле состояния элемента таблицы

db 02dh форматирование вывода на экран key db 10 dup (' ') :ключ. он же значение константы

db 02dh форматирование вывода на экран

line db 2 dup (' ') :строка файла, в которой встретилась константа endjine db Odh.Oah.'S' :для удобства вывода на экран ends .data

s_tab state_tab <> tab constant 19 dup (<>)

constant <8.> последний элемент таблицы - бит 3=1 end_tab=$-tab

filename db 'maket.txf.0 handle dw 0 : дескриптор файла buf db 240 dup С ') xlat_tab db Odh dup (OO).Odh ;признак конца строки

db 'O'-Oeh dup (0)

db ':'-'0'+l dup CO') ;признак цифры 0..9

db 'H'-':' dup (0). " :признак буквы 'Н'

db 'h'-'H' dup (0). 'h' ;признак буквы 'h' db Offh-'h1 dup (00)

curjine db 0

.code

:открываем файл mov ah. 3dh

movdx,offset filename

int 21h

jc exit :ошибка (cf=l)

mov handle.ax ;читаем файл:

movah.3fh :функция установки указателя

mov bx,handle

mov ex,240 ;читаем максимум 240 байт

lea dx.buf

int 21h

jc exit

mov ex.ax фактическая длина файла в сх инициализируем дескриптор таблицы s_tab

lea si.tab :адрес таблицы в si

mov s_tab.elem_fгее.si ;первый элемент таблицы - свободен

add si .end_tab

mov s_tab.last_off,si :адрес первого байта за концом таблицы

lea bx.xlat_tab

leadi. buf

cканируем до первого пробела: push ds popes

cycll: mov al. ' ' repne scasb -.сканирование до первого пробела

jcxz displ .цепочка отсканирована -> таблица заполнена push сх :классифицируем символ после пробела (команда XLAT):

mov al.[di]

xlat

emp al. '0':первый символ после пробела - 0

je ml

cmpal.Odh :первый символ после пробела - Odh

je m2 :все остальное либо идентификаторы, либо неверно записанные числа

pop сх

jmpcycll ml: :первый символ после пробела - 0..9:

mov si.di ;откуда пересылать

fmov al. ' ' push di repne scasb сканирование до первого пробела mov cx.di dec ex subcx.si ;сколько пересылать lea di.tab emp s__tab.elem_free.0ffffh :есть свободные элементы? je displ : свободных элементов нет

mov di,s_tab.elem_free :адрес первого свободного элемента push di

lea di.[di].key rep movsb ;пересыпаем в элемент таблицы

deed! ;Какого типа это константа?

emp byte ptr [di].'h' popdi

je m4

and [di].state.Ofbh ;десятичная константа

jmp $+5 m4: or [di].state.100b ;шестнадцатеричная константа

mov al ,cur_line :текущий номер строки в al

aam преобразуем в символьное представление

or ah.030h

mov [di].line,ah

or al.030h

mov [di+1].line.al :и в элемент таблицы

or [di].state.lb ;помечаем элемент как используемый

:теперь нужно поместить в поле s_tab. elem_free адрес нового свободного элемента пб: emp di. s_tab. 1 ast_of f

ja displ

add di.type constant :к следующему элементу

test [di].state.lb

jnz m5 ; используется => к следующему элементу

mov s_tab.elem_fгее.d i pop di pop ex

jmpcycU m2: увеличить номер строки

inc cur_line

jmp cycl 1 displ: :отображение на экране элементов таблицы

lea di .tab m6:

test [di].state.100b

jnz m7 :выводим на экран строку

mov ah.9

mov dx.di

int 21h ml: add di. type constant

emp di ,s_tab.last_off

jb m6

В этой программе показаны основные приемы работы с неупорядоченной таблицей. Усложнить данную программу можно, например, дополнив набор сведений о каждой константе информацией о ее длине. Далее можно попрактиковаться в этом вопросе, поставив себе задачу удалить из таблицы данные о нулевых константах (обоих типов — 0 и 0h) и вывести окончательное содержимое таблицы на экран. В качестве ключа для доступа к ячейке таблицы можно использовать значение самой константы (размером 10 байт).

Обратите внимание на еще два момента, отраженные в этой программе.

Использование команды XLAT для классификации символов в качестве цифр и остальных символов (букв). Среди других кодов в таблице перекодировки особо выделен байт со значением Odh, который является первым байтом в паре OdOah. Как вы помните, эта пара вставляется редакторами ASCII-текстов для обозначения конца строки и перехода на другую строку.

Организация таблицы. Ей предшествует четырехбайтовый префикс, содержащий информацию о конце таблицы и первом свободном элементе таблицы. В целях оптимизации область памяти для буфера buf и таблицы перекодировки лучше выделять динамически и после анализа файла удалять.

Древовидные таблицы

Древовидные таблицы являются несколько улучшенным вариантом неупорядоченных таблиц. Новые записи в древовидную таблицу по-прежнему поступают неупорядоченно. Но на этот раз место, занимаемое этими записями среди других записей в таблице, определяется значением ключевого поля. Принцип здесь такой же, как и в сортировке с помощью дерева (см. материал выше).

В общем случае каждая запись в древовидной таблице сопровождается двумя указателями (Рисунок 2.7): один указатель хранит адрес записи с меньшим значением ключа (адрес узла-предка), второй — с большим (адрес узла-сына).

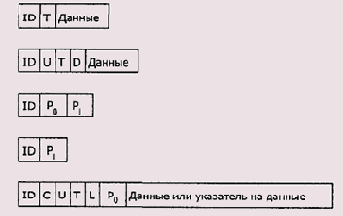
Рисунок 2.7. Древовидная организация таблицы

Процесс добавления нового элемента в древовидную таблицу производится следующим образом. Значение ключа нового элемента сравнивается со значением ключа первого элемента дерева. По результатам сравнения ключей новый элемент «поступает» в левое или правое поддерево первого элемента дерева. Далее процесс сравнения и поступления в левое или правое поддерево очередного узла продолжается аналогичным образом и до тех пор, пока не будет найден пустой элемент в нужном направлении просмотра. Новая запись помещается в данный пустой элемент, при этом настраивается указатель с адресом узла-предка.

Преимущества древовидной структуры таблицы проявляются на этапе поиска нужного элемента. Сам процесс подобен действиям на этапе вставки нового элемента в таблицу, являясь при этом в отличие от неупорядоченного поиска целенаправленным. Поиск прекращается либо при совпадении ключевого поля, либо при обнаружении пустого указателя, то есть это означает, что нужного элемента в таблице нет.

Самое сложное в использовании древовидных таблиц — реализация процесса удаления элементов, так как при этом необходимо производить их переупорядочивание.

Реализовать таблицу древовидной организации можно как с использованием полей указателей (см. выше), так и без них. Если отказаться от полей указателей, то таблица может представлять собой массив из п структур, которые пронумерованы от 0 до п-1. Тогда структура с ключом, соответствующим корню дерева, должна располагаться на месте структуры с номером m = [(n-1)/2], где скобки [] означают целую часть от деления. Соответственно левое поддерево будет располагаться в левом подмассиве (элементы 0..m-1), а правое — в правом подмассиве (элементы m+1..n-1). Корень левого поддерева — элемент ш,' - [(m-1)/2], корень правого поддерева — элемент mr = [т+1+(п-1)/2] и т. д. Этот способ экономичнее с точки зрения расходования памяти, но сложнее алгоритмически. Предполагается, что соответствующее таблице дерево сбалансировано и максимальное количество элементов в таблице известно.

Наглядный пример организации древовидной таблицы — расстановка слов в лексикографическом порядке. Эта операция выполняется с помощью лексикографических деревьев, понятие о которых приведено ниже — в разделе, посвященном деревьям. Там же приведен соответствующий пример.

Упорядоченные таблицы

Работа с таблицей оказывается более эффективной, если элементы в ней некоторым образом упорядочены. Наиболее часто таблица упорядочивается по значению ключевого поля. Но не исключено и использование другого принципа упорядочивания, к примеру по частоте обращения к элементам таблицы и т. п. Упорядочивание таблицы и последующий поиск в ней производится методами, рассмотренными выше. Порядок выполнения этих и других операций с упорядоченной по значению ключа таблицей рассмотрим на следующем примере.

Пусть необходимо запомнить элементы таблицы информацией о 10 словах, вводимых с клавиатуры. Длина слов — не более 20 символов. Структура элемента таблицы следующая: поле с количеством символов в слове; поле с самим словом. После ввода информации о словах необходимо упорядочить элементы таблицы по признаку длины слов. Затем вывести на экран элемент таблицы, содержащий первое из слов длиной 5 символов, удалить этот элемент из таблицы и вставить в нее новое слово, введенное с клавиатуры.

При такой постановке задачи нам придется решить весь комплекс проблем, возникающих при работе с упорядоченными таблицами.

:prg02_06.asm - программа на ассемблере демонстрации работы с упорядоченной таблицей

;Вход: 10 слов, вводимых с клавиатуры. Длина слов - не более 20 символов.

;Выход: вывод на экран элемента таблицы, содержащего первое из слов длиной 5 символов,

удаление этого элемента из таблицы и вставка в нее нового слова, введенного с

клавиатуры.

element tab struc

lendb 0 -.длина слова

simvjd db 20 dup (20h) :само слово

ends

0длина введенного слова (без учета 0dh) К db 21 dup (20h) -.буфер для ввода (с учетом 0dh)регистры

lea si.in_str -.откуда пересылать

Tea di out_str ;куда пересылать

movcx.lenjnovs -.сколько пересылать repmevsb ; пересылаем строку восстанавливаем регистры

tabelement._tab 10 dup (<>)

len_tab=$-tab

buf buf_0ah<>

key db 5

nrev element tab <> ;предыдущий элемент

Г element tab" <> временная переменная для сортировки

.code

leadi.tab lea si .buf . bufjn mov ex. 10 lea dx. buf movah.Oah push ds

mh ;вводим слова с клавиатуры в буфер buf

-.сохраняем регистры .........

intZlh

move1, buf. lenjn

mov [di].len.cl ;длина слова -> tab.length

adddi ,simv id

repmovsb -.пересылка слова в элемент таблицы :восстанавливаем регистры .........

adddi.type element_tab

;Упорядочиваем таблицу методом пузырьковой сортировки

п-10

mov cx.n-1

mov si .1

@@сус11: :внешний цикл - по 1 push ex

subcx'.S! количество повторений внутреннего цикла push si временно сохраним 1 - теперь о=п

mov si .n-1

@@cyc!2: push si

movax.type element_tab

mul si

mov si.ax

mov di .si

sub di.type element_tab :в di адрес предыдущей записи

mov al.[di].len

cmp [si].len.al сравниваем последующий с предыдущим

ja @@ml ;обмениваем

s_movsbx.[di].<type element_tab> :x=mas[j-l]

s_movsb[di].[si].<type element_tab> ;mas[j-l]»mas[j] ;mas[j]=x push ex

mov ex.type element_tab :сколько пересылать

mov di ,si

lea si.x юткуда пересылать repmovsb : пересылаем строку pop ex @@ml: pop si

dec si :цикл по j с декрементом n-i раз

loop @@cycl2 pop si

inc si pop ex

dec ex

jcxz in2

jmp @@cycl 1

m2: ;ищем элемент путем двоичного поиска :в si и di индексы первого и последнего элементов последней просматриваемой части

последовательности;

mov si.0

mov di.n-1

;получим центральный индекс: cont_search: cmp si .di :проверка на окончание (неуспешное):si>di

ja exit

mov bx.si

add bx.di

shr bx.l ; делим на 2 push bx

movax.type element_tab

mul bx

mov bx.ax

mov al.key :искомое значение в ах

cmp [bx].Ten.al сравниваем с искомым значением

je @@rn4 ; искомое значение найдено

ja ШтЗ :[bx].len>k ;[bx].len<k: popbx

mov si ,bx

inc si

jmpcont_search @@m3: pop bx :1

mov di .bx

dec di

jmp cont_search @@m4: movax.type element_tab

mul si

mov si.ax

: конец поиска - в si адрес элемента таблицы со словом длиной 5 байт :выводим его на экран :преобразуем длину в символьный вид:

mov al, [si]. Ten

хог ex.ex

movcl.al ;длина для movsb

aam

or ах. ;в ах длина в символьном виде

mov buf. 1 en_buf.ah

mov buf .lerMn.al push si :сохраним указатель на эту запись

add si .simvjd

lea di .buf.buf_in rep movsb

mov byte ptr [di].'$' :конец строки для вывода 09h (int 21h) :теперь выводим:

lea dx.buf

mov ah.09h

int 21h

:удаляем запись pop si :-i- восстановим указатель на удаляемую запись

mov di .si

add si .type element_tab

mov cx.len_tab

sub ex.si ;в сх сколько пересылать rep movsb :обнуляем последнюю запись

xor al .al

mov ex.type element_tab rep stosb

:вводим слово с клавиатуры: insert: ;вводим слово с клавиатуры lea dx.buf mov ah.0ah int21h :c помощью линейного поиска ищем место вставки, в котором выполняется условие buf.1еn_

in=<[si].Ten

lea si.tab

mov al .buf.len_in @@m5: emp al,[si].Ten

jbe @@m6

add si .type element_tab

jmp @@m5

@@m6: push si сохраняем место вставки :раздвигаем таблицу, последний элемент теряется

add si.type element_tab

mov cx.len_tab

sub ex.si ;сколько пересылать std

lea si .tab

add si , lentab

mov di.si

sub si.type element_tab rep movsb eld

;формируем и вставляем новый элемент pop di восстанавливаем место вставки :обнуляем место вставки push di

хог al .al

mov ex.type element_tab rep stosb popdi

lea si ,buf .bufjn

mov cl .buf .lenjn

mov [di].len,cl

add di ,simv_id rep movsb

Таблицы с вычисляемыми входами

Ранее мы отмечали, что скорость доступа к элементам таблицы зависит от двух факторов — способа организации поиска нужного элемента и размера таблицы. Для маленьких таблиц любой метод доступа будет работать быстро. С ростом размера таблицы выбор способа организации доступа приходится производить прежде всего исходя из критерия скорости локализации нужного элемента таблицы. Элементы таблицы отличаются друг от друга уникальным значением ключевого поля. При этом ключевыми могут являться не только одно, но и несколько полей элемента таблицы. Ключ, в том числе и символьный, в памяти представляется последовательностью двоичных байт. Исходя из того что ключ уникален, соответствующая двоичная последовательность также будет уникальной. А нельзя ли использовать это уникальное значение ключа для вычисления адреса местоположения элемента в таблице? Оказывается, можно, а в ряде приложений это оказывается очень эффективно, так как в идеальном случае доступ к нужному элементу таблицы осуществляется всего за одно обращение к памяти. С другой стороны, на практике часто возникает необходимость размещения элементов таблицы с достаточно большим диапазоном возможных значений ключевого поля, в то время как программа реально использует лишь небольшое подмножество значений этих ключей. Например, значение ключевого поля может быть в диапазоне 0..3999, но задача постоянно использует не более 50 значений. В этом случае крайне неэффективным было бы резервировать память для таблицы размером в 4000 элементов, а реально использовать чуть больше 1 % отведенной для нее памяти. Гораздо лучше иметь возможность воспользоваться некоторой процедурой, отображающей задействованное пространство ключей на таблицу размером, близким к значению 50. Большинство подобных задач решается с использованием методики, называемой хэшированием. Ее основу составляют различные алгоритмы отображения значения ключа в значение адреса размещения элемента в таблице. Непосредственное преобразование ключа в адрес производится с помощью функций расстановки, или хэш-функций. Адреса, получаемые из ключевых слов с помощью хэш-функций, называются хэш-адресами. Таблицы, для работы с которыми используются методы хеширования, называются таблицами с вычисляемыми входами, хэш-таблицами, или таблицами с прямым доступом.

Основополагающую идею хэширования можно пояснить на следующем примере. Предположим, необходимо подсчитать, сколько раз в тексте встречаются слова, первый символ которых — одна из букв английского алфавита (или русского — это не имеет значения, можно в качестве объекта подсчета использовать любой символ из кодовой таблицы). Для этого в памяти нужно организовать таблицу, количество элементов в которой будет соответствовать количеству букв в алфавите. Далее необходимо составить программу, в которой текст будет анализироваться с помощью цепочечных команд. При этом нас интересуют разделяющие слова пробелы и первые буквы самих слов. Так как символы букв имеют определенное двоичное значение, то на его основе вычисляется адрес в таблице, по которому располагается элемент, в минимальном варианте состоящий из одного поля. В этом поле ведется подсчет количества слов в тексте, начинающихся с данной буквы. В следующей программе с клавиатуры вводится 20 слов (длиной не более 10 символов), производится подсчет английских слов, начинающихся с определенной строчной буквы, и результат подсчета выводится на экран. Хэш-функция (функция расстановки) имеет вид:

A=(C-97)*L,

где А — адрес в таблице, полученный на основе двоичного значения символа С; L — длина элемента таблицы (для нашей задачи L=l); 97 — десятичное смещение в кодовой таблице строчного символа «а» английского алфавита.

:prg02_07.asm - программа на ассемблере для подсчета количества слов, начинающихся

с определенной строчной буквы

:Вход: ввод с клавиатуры 20 слов (длиной не более 10 символов). -.Выход: вывод результата подсчета на экран.

buf_Oahstruc

len_bufdb 11 ; длина bufjn

lenjin db 0 действительная длина введенного слова (без учета Odh) bufjn db 11 dup (20h) -.буфер для ввода (с учетом Cdh) ends 1 .data

tabdb 26 dup (0) buf buf_0ah<>

db Odh.Oah,'$' ;для вывода функцией 09h (int 21h)

.code

-.вводим слова с клавиатуры

mov ex,20

lea dx.buf

movah.Oah ml: int 21h :анализируем первую букву введенного слова - вычисляем хэш-функцию: А=С*1-97

mov Ы , buf . bufjn sub Ы. 97 inc [bx] loop ml

:выводим результат подсчета на экран push ds popes

xor al ,al

lea di ,buf

mov ex.type bufjah rep stosb ; чистим буфер buf

mov ex.26 :синвол в buf.buf_1n

lea dx.buf

mcv Ы,97 m2: push bx

mov buf .bufjn.bi :опять вычисляем хэш-функцию:

А»С*1-97 и преобразуем "количество" в символьный вид

sub Ы. 97

mov al .[bx]

aam

or ax,03030h ;в ах длина в символьном виде

mov buf.len in.al —

mov buf.len_buf.ah ;теперь выводим:

mov ah, 09h

int 21h pop bx

inc Ы

loop m2

Таким образом, относительно сложная с первого взгляда задача очень просто реализуется с помощью методов хэширования. При этом обеспечивается высокая скорость выполнения операций доступа к элементам таблицы. Это обусловлено тем, что адреса, по которым располагаются элементы таблицы, являются результатами вычислений простых арифметических функций от содержимого соответствующих ключевых слов.

Перечислим области, где методы хэширования оказываются особенно эффективными.

Разработка компиляторов, программ обработки текстов, пользовательских интерфейсов и т. п. В частности, компиляторы значительную часть времени обработки исходного текста программы затрачивают на работу с различными таблицами — операций, идентификаторов, констант и т. д. Правильная организация работы компилятора с информацией в этих таблицах означает значительное увеличение скорости создания объектного модуля, может быть, даже не на один порядок выше. Кстати, другие системные программы — редакторы связей и загрузчики — также активно работают со своими внутренними таблицами.

Системы управления базами данных. Здесь особенный интерес представляют алгоритмы выполнения операций поиска по многим ключам, которые также основаны на методе хэширования.

Разработка криптографических систем.

Поиск по соответствию. Методы хэширования можно применять в системах распознавания образов, когда идентификация элемента в таблице осу ществляется на основе анализа ряда признаков, сопровождающих объект поиска, а не полного соответствия заданному ключу. Если рассматривать эту возможность в контексте задач системного программирования, то ее можно использовать для исправления ошибок операторов при вводе информации в виде ключевых слов. Подробная информация о поиске по соответствию приведена в литературе.

Но на практике не все так гладко и оптимистично. Для эффективной и безотказной работы метода хэширования необходимо очень тщательно подходить как к изучению задачи на этапе ее постановки, так и к возможности использования конкретного алгоритма хэширования в контексте этой задачи. Так, на стадии изучения постановки задачи, в которой для доступа к табличным данным планируется использовать хэширование, требуется проводить тщательные исследования по направлениям: диапазон допустимых ключей, максимальное количество элементов в таблице, вероятность возникновения коллизий и т. д. При этом нужно знать как общие проблемы метода хэширования, так и частные проблемы конкретных алгоритмов хэширования. Одну из таких проблем рассмотрим на примере задачи.

Пусть необходимо подсчитать количество двухсимвольных английских слов в некотором тексте. В качестве хэш-функции для вычисления адреса можно предложить функцию подсчета суммы двух символов, умноженной на длину элемента таблицы: A=(Cl+C2)*L-97, где А — адрес в таблице, полученный на основе суммы двоичных значений символов С1 и С2; L — длина элемента таблицы; 97 — десятичное смещение в кодовой таблице строчного символа «а» английского алфавита. Проведем простые расчеты. Сумма двоичных значений двух символов 'а' равна 97+97=194, сумма двоичных значений двух символов 'г' равна 122+122=244. Если организовать хэш-таблицу, как в предыдущем случае, то получится, что в ней должно быть всего 50 элементов, чего явно недостаточно. Более того, для сочетаний типа ab и Ьа хэш-сумма соответствует одному числовому значению. В случае когда функция хэширования вычисляет одинаковый адрес для двух и более различных объектов, говорят, что произошла коллизия, или конфликт. Исправить положение можно введением допущений и ограничений, вплоть до замены используемой хэш-функции.

Программист может либо применить один из известных алгоритмов хэширования (что, по сути, означает использование определенной хэш-функции), либо изобрести свой алгоритм, наиболее точно отображающий специфику конкретной задачи. При этом необходимо понимать, что разработка хэш-функции происходит в два этапа.

1. Выбор способа перевода ключевых слов в числовую форму.

2. Выбор алгоритма преобразования числовых значений в набор хэш-адресов.

Выбор способа перевода ключевых слов в числовую форму

Вся информация, вводимая в компьютер, кодируется в соответствии с одной из систем кодирования (таблиц кодировки). В большинстве таких систем символы (цифры, буквы, служебные знаки) представляются однобайтовыми двоичными числами. В последних версиях Windows (NT, 2000) используется система кодировки Unicode, в которой символы представляются в виде двухбайтовых двоичных величин. Как правило, ключевые поля элементов таблиц — строки символов, Наиболее известные алгоритмы закрытого хэширования основаны на следующих методах [32]:

деления;

умножения;

извлечения битов;

квадрата;

сегментации;

перехода к новому основанию;

алгебраического кодирования;

вычислении значения CRC (см. соответствующую главу).

Далее мы рассмотрим только первые четыре метода. Остальные методы — сегментации, перехода к новому основанию, алгебраического кодирования — мы рассматривать не будем. Отметим лишь, что их используют либо в случае значительной длины ключевых слов, либо когда ключ состоит из нескольких слов. Информацию об этих методах можно получить в литературе .

Рассмотрение методов хэширования будет произведено на примере одной задачи. Это позволит лучше понять их особенности, преимущества, недостатки и возможные ограничения.

Необходимо разработать программу — фрагмент компилятора, которая собирает информацию об идентификаторах программы. Предположим, что в программе может встретиться не более М различных имен. Длину возможных имен ограничим восьмью символами. В качестве ключа используются символы идентификатора, какие и сколько — будем уточнять для каждого из методов. Элемент таблицы состоит из 10 байт: 1 байт признаков, 1 байт для хранения длины идентификатора и 8 байт для хранения символов самого идентификатора.

Метод деления

Этот простой алгоритм закрытого хэширования основан на использовании остатка деления значения ключа К на число, равное или близкое к числу элементов таблицы М:

А(К) = К mod M

В результате деления образуется целый остаток А(К), который и принимается за индекс блока в таблице. Чтобы получить конечный адрес в памяти, нужно полученный индекс умножить на размер элемента в таблице. Для уменьшения коллизий необходимо соблюдать ряд условий:

Значение М выбирается равным простому числу.

Значение М не должно являться степенью основания, по которому производится перевод ключей в числовую форму. Так, для алфавита, состоящего из первых пяти английских букв и пробела {a,b,c,d,e,' '} (см. пример выше), основание системы равно 6. Исходя из этого число элементов таблицы М не должно быть степенью 6Р.

Важно отметить случай, когда число элементов таблицы М является степенью основания машинной систем счисления (для микропроцессора Intel — это 2). Тогда операция деления (достаточно медленная) заменяется на несколько операций.

Метод умножения

Для этого метода нет ограничений на длину таблицы, свойственных методу деления. Вычисление хэш-адреса происходит в два этапа:

1. Вычисление нормализованного хэш-адреса в интервале [0..1] по формуле:

F(K) = (С*К) mod 1,

где С — некоторая константа из интервала [0..1], К — результат преобразования ключа в его числовое представление, mod 1 означает, что F(K) является дробной частью произведения С*К.

2. Конечный хэш-адрес А(К) вычисляется по формуле А(К) = [M*F(K)], где М — размер хэш-таблицы, а скобки [] означают целую часть результата умножения.

Удобно рассматривать эти две формулы вместе:

А(К) = М*(С*К) mod 1. (2.4)

Кнут в качестве значения С рекомендует использовать «золотое сечение» — величину, равную ((л/5)-1)/2«0,6180339887. Значение F(K) можно формировать с помощью как команд сопроцессора, так и целочисленных команд. Команды сопроцессора вам хорошо известны и трудностей с реализацией формулы (2.4) не возникает. Интерес представляет реализация вычисления А(К) с помощью целочисленных команд. Правда, в отличие от реализации сопроцессором здесь все же Удобнее ограничиться условием, когда М является степенью 2. Тогда процесс вычисления с использованием целочисленных команд выглядит так:

Выполняем произведение С*К. Для этого величину «золотого сечения» С~0, 6180339887 нужно интерпретировать как целочисленное значение,

обходимо стремиться к тому, чтобы появление 0 и 1 в выделяемых позициях было как можно более равновероятным. Здесь трудно дать рекомендации, просто нужно провести анализ как можно большего количества возможных ключей, разделив составляющие их байты на тетрады. Для формирования хэш-адреса нужно будет взять биты из тех тетрад (или полностью тетрады), значения в которых изменялись равномерно.

Метод квадрата

В литературе часто упоминается метод квадрата как один из первых методов генерации последовательностей псевдослучайных чисел. При этом он непременно подвергается критике за плохое качество генерируемых последовательностей. Но, как упомянуто выше, для процесса хэширования это не является недостатком. Более того, в ряде случаев это наиболее предпочтительный алгоритм вычисления значения хэш-функции. Суть метода проста: значение ключа возводится в квадрат, после чего берется необходимое количество средних битов результата. Возможны варианты — при различной длине ключа биты берутся с разных позиций. Для принятия решения об использовании метода квадрата для вычисления хэш-функции необходимо провести статистический анализ возможных значений ключей. Если они часто содержат большое количество нулевых битов, то это означает, что распределение значений битов в средней части квадрата ключа недостаточно равномерно. В этом случае использование метода квадрата неэффективно.

На этом мы закончим знакомство с методами хэширования, так как полное обсуждение этого вопроса не является предметом книги. Информацию об остальных методах (сегментации, перехода к новому основанию, алгебраического кодирования) можно получить из различных источников.

В ходе реализации хэширования с помощью методов деления и умножения возможные коллизии мы лишь обозначали без их обработки. Настало время разобраться с этим вопросом.

Обработка коллизий

Для обработки коллизий используются две группы методов:

закрытые — в качестве резервных используются ячейки самой хэш-таблицы;

открытые — для хранения элементов с одинаковыми хэш-адресами используется отдельная область памяти.

Видно, что эти группы методов разрешения коллизий соответствуют классификации алгоритмов хэширования — они тоже делятся на открытые и закрытые. Яркий пример открытых методов — метод цепочек, который сам по себе является самостоятельным методом хэширования. Он несложен, и мы рассмотрим его несколько позже.

Закрытые методы разрешения коллизий более сложные. Их основная идея — при возникновении коллизии попытаться отыскать в хэш-таблице свободную ячейку. Процедуру поиска свободной ячейки называют пробитом, или рехэшировани-ем (вторичным хэшированием). При возникновении коллизии к первоначальному хэш-адресу А(К) добавляется некоторое значение р, и вычисляется выражение (2.5). Если новый хэш-адрес А(К) опять вызывает коллизию, то (2.5) вычисляется при р2, и так далее:

А(К) = (A(K)+Pi)mod М (I = 0..М). (2.5)

push ds popes

lea si .buf.len_in

mov cl .buf .lenjn

inccx :длину тоже нужно захватить

add di .lenjd repmovsb

jmp ml displ: :выводим идентификатор, вызвавший коллизию, на экран

рехэширование

;ищем место для идентификатора, вызвавшего коллизию в таблице, путем линейного рехэширования i nc bx mov ax.bx jmp m5

Квадратичное рехэширование

Процедура квадратичного рехэширования предполагает, что процесс поиска резервных ячеек производится с использованием некоторой квадратичной функции, например такой:

Pi = а,2+Ь,+с. (2.6)

Хотя значения а, Ь, с можно задавать любыми, велика вероятность быстрого зацикливания значений р(. Поэтому в качестве рекомендации опишем один из вариантов реализации процедуры квадратичного рехэширования, позволяющий осуществить перебор всех элементов хэш-таблицы [32]. Для этого значения в формуле (2.6) положим равными: а=1,Ь = с = 0. Размер таблицы желательно задавать равным простому числу, которое определяется формулой М = 4п+3, где п — целое число. Для вычисления значений р> используют одно из соотношений:

pi = (K+i2)modM. (2.7)

Pi = [M+2K-(K+i2)modM]modM. (2.8)

где i = 1, 2, ..., (M-l)/2; К — первоначально вычисленный хэш-адрес.

Адреса, формируемые с использованием формулы (2.7), покрывают половину хэш-таблицы, а адреса, формируемые с использованием формулы (2.8), — вторую половину. Практически реализовать данный метод можно следующей процедурой.

1. Задание I = -М.

2. Вычисление хэш-адреса К одним из методов хэширования.

3. Если ячейка свободна или ключ элемента в ней совпадает с искомым ключом, то завершение процесса поиска. Иначе, 1:=1+1.

4. Вычисление h := (h+|i|)modM.

5. Если I < М, то переход к шагу 3. Иначе (если I > М), таблица полностью заполнена.

Программа та же, что приведена в методе линейного рехэширования, за исключением добавления одной команды для инициализации процесса рехэширования, самого фрагмента рехэширования и небольших изменений сегмента данных. могут являться методы, основанные на деревьях поиска, и т. п. Наибольший эффект от хеширования — при поиске по заданным идентификаторам или дескрипторам, что характерно для задач баз данных, обработки документов и т. д. Для задач, в которых поиск ведется сравнением или вычислением сложных логических функций, лучше использовать традиционные методы сортировки и поиска.

Для того чтобы совершить плавный переход к рассмотрению следующей структуры данных — спискам, вернемся еще раз к одной проблеме, связанной с массивами. Упоминалось, что среди массивов можно выделить массивы специального вида, которые называют разреженными. В этих массивах большинство элементов равны нулю. Отводить место для хранения всех элементов расточительно. Естественно, возникает желание сэкономить. Что для этого можно предпринять?

Техника обработки массивов предполагает, что все элементы расположены в соседних ячейках памяти. Для ряда приложений это недопустимое ограничение.

Обобщенно можно сказать, что все перечисленные выше структуры имеют общие свойства:

постоянство структуры данных на всем протяжении ее существования;

память для хранения отводится сразу всем элементам структуры и все элементы находятся в смежных ячейках памяти;

отношения между элементами просты настолько, что можно исключить потребность в средствах хранения информации об их отношениях в какой бы то ни было форме.

Исходя из этих свойств данные структуры данных и называют статическими. Снять подобные ограничения можно, используя другой тип данных — списки. Для них подобных ограничений не существует.

Последовательные списки

Если количество элементов в списке постоянно, то в зависимости от их типа список вырождается в вектор, массив, структуру или таблицу. Отличие списка от этих структур данных — в длине. Для списков она является переменной. Поэтому программист, разбираясь с самими списками, должен уделить внимание тому, каким образом ему следует выделять память для хранения списка. Обычно языки высокого уровня имеют соответствующие средства в отличие от языка ассемблера. При написании программы на ассемблере программист должен уметь напрямую обратиться к операционной системе для решения проблемы динамического управления памятью. В примерах мы будем использовать соответствующие функции API Win32 как более современные, хотя для общего случая это не принципиально. В MS DOS имеются аналогичные функции (с точки зрения цели использования) — это функции 48h, 49h, 4ah прерывания 21h. Вопрос динамического управления памятью в силу своей важности в контексте настоящего рассмотрения требует особого внимания.

Отличие последовательных списков от связных состоит в том, что добавление и удаление элементов возможно только по концам структуры. В зависимости от алгоритма изменения различают такие виды последовательных списков, как стеки, очереди и деки. Эти виды списков обычно дополняются служебным дескриптором, который может содержать указатели на начало и конец области памяти, выделенной для списка, указатель на текущий элемент.

Зачем нужен, к примеру, стек? Необходимость использования своего стека в программе вполне вероятна, хотя бы исходя из того, что элементы, для хранения которых он создается, могут иметь размер, отличный от 2/4 байта.

Важно понимать, что внутренняя структура элемента практически не зависит от типа последовательного списка. Списки отличает набор операций, которые производятся над ними. Поэтому рассмотрим их отдельно для каждого типа последовательного списка.

Построение двоичного дерева

Как уже отмечалось выше, для реализации двоичного поиска необходим упорядоченный массив чисел. Поэтому уже на этапе построения двоичное дерево необходимо специальным образом организовать. Двоичное дерево поиска организуется так, что между его узлами существуют следующие соотношения: для каждого узла а, все элементы левого поддерева меньше а, а элементы правого поддерева больше либо равны а.

:prg02_12.asm - программа построения и инициализации двоичного дерева.

:Вход: произвольный массив чисел в памяти.

:Выход: двоичное дерево в памяти.

;объявления структур:

node_tree struc :узел дерева

simbol db 0 содержательная часть

l_son dd 0 указатель на старшего (левого) сына

r_son dd 0 указатель на младшего (правого) сына

ends

.data

mas db 37h.12h.8h.65h.4h.54h.llh.02h.32h.5h.4h.87h.7h.21h.65h.45h.22h.

Ilh,77h.51h,26h.73h.35h.l2h.49h.37h.52h l_mas=$-mas

.code

BuildBinTree proc

формируем корень дерева и указатель на дерево HeadTree

:для размещения дерева используем кучу, выделяемую процессу по умолчанию (1 Мбайт).

:но при необходимости можно создать и доп. кучу с помощью HeapCreate

iHANDLE GetProcessHeap (VOID):

call GetProcessHeap

movHand_Head,eax сохраняем дескриптор ;запрашиваем и инициализируем блок памяти из кучи для корня дерева:

xorebx.ebx :здесь будет указатель на предыдущий узел ;LPVOID HeapAllос(HANDLE hHeap, DWORD dwFlags, DWORD dwBytes):

push type node_tree :размер структуры для узла дерева

push 0 ;флаги не задаем

push eax :описатель кучи (он же в Hand_Head)

call НеарАПос

mov HeadTree.eax запоминаем указатель на корень дерева

mov ebx.eax :и в ebx :подчистим выделенную область памяти в куче

push ds

pop es

mov edi .eax

mov ecx.type node_tree

mov al .0 rep stosb

leaesi.mas ;первое число из mas в корень дерева

lodsb ;число в al

mov [ebx].simbol.al

mov ecx.l_mas-l @@cycll: ;далее в цикле работаем с деревом и массивом mas

push ecx ;НеарА11ос портит ecx. возвращая в нем некоторое значение ;запрашиваем блок памяти из кучи для узла дерева: ;LPVOID HeapAllос(HANDLE hHeap. DWORD dwFlags, DWORD dwBytes);

Построение двоичного дерева

:prg02_12.asm - программа построения и инициализации двоичного дерева.

:Вход: произвольный массив чисел в памяти.

:Выход: двоичное дерево в памяти.

;объявления структур:

node_tree struc :узел дерева

simbol db 0 содержательная часть

l_son dd 0 указатель на старшего (левого) сына

r_son dd 0 указатель на младшего (правого) сына

ends

.data

mas db 37h.12h.8h.65h.4h.54h.llh.02h.32h.5h.4h.87h.7h.21h.65h.45h.22h.

Ilh,77h.51h,26h.73h.35h.l2h.49h.37h.52h l_mas=$-mas

.code

BuildBinTree proc

формируем корень дерева и указатель на дерево HeadTree

:для размещения дерева используем кучу, выделяемую процессу по умолчанию (1 Мбайт).

:но при необходимости можно создать и доп. кучу с помощью HeapCreate

iHANDLE GetProcessHeap (VOID):

call GetProcessHeap

movHand_Head,eax сохраняем дескриптор ;запрашиваем и инициализируем блок памяти из кучи для корня дерева:

xorebx.ebx :здесь будет указатель на предыдущий узел ;LPVOID HeapAllос(HANDLE hHeap, DWORD dwFlags, DWORD dwBytes):

push type node_tree :размер структуры для узла дерева

push 0 ;флаги не задаем

push eax :описатель кучи (он же в Hand_Head)

call НеарАПос

mov HeadTree.eax запоминаем указатель на корень дерева

mov ebx.eax :и в ebx :подчистим выделенную область памяти в куче

push ds

pop es

mov edi .eax

mov ecx.type node_tree

mov al .0 rep stosb

leaesi.mas ;первое число из mas в корень дерева

lodsb ;число в al

mov [ebx].simbol.al

mov ecx.l_mas-l @@cycll: ;далее в цикле работаем с деревом и массивом mas

Представление дерева в памяти

Естественным является представление дерева в памяти компьютера в форме многосвязного списка. Это наиболее динамичное представление. В случае постоянства структуры дерева могут использоваться и другие способы представления дерева в памяти, например в виде массива, как это было во время рассмотрения нами двоичной сортировки. В случае представления дерева в форме многосвязного списка указатель на начало списка должен указывать на элемент списка, являющийся корнем. В свою очередь, узлы дерева связываются между собой так, чтобы корень дерева был связан с корнями его поддеревьев и т. д. При этом можно выделить три случая.

Связь узлов в дереве осуществляется таким образом (Рисунок 2.19, а), что каждый узел-сын содержит ссылку на вышестоящий узел (узел-отца). В этом случае корень будет содержать нулевой указатель на месте соответствующего указателя. Имея такой тип связей узлов в дереве, можно подниматься от нижних уровней дерева к его корню, что может быть полезным при реализации определенных видов синтаксического разбора.

Каждый узел дерева содержит указатели на свои поддеревья (Рисунок 2.19, б), то есть каждый отец ссылается на своих сыновей. Этот способ применим для представления деревьев небольшой арности, например бинарных деревьев. Имея указатель на корень дерева, можно достичь любого узла дерева.

Каждый узел дерева ссылается на свои поддеревья с помощью списка, при этом каждый узел содержит два указателя — для представления списка поддеревьев и для связывания узлов в этот список (Рисунок 2.19, е).

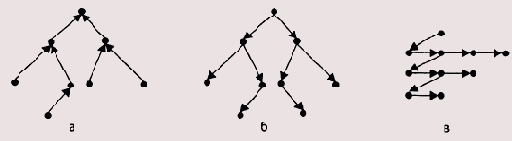
Рисунок 2.19. Варианты связи узлов дерева между собой

Бинарное дерево обычно представляется с помощью второго способа (Рисунок 2.19, б). Минимально для представления узла достаточно трех полей: содержательной части узла и двух указателей — на левого (старшего) и правого (младшего) сыновей. Таким образом, представить бинарное двоичное дерево можно с помощью нелинейного двусвязного списка. Структуру узла в программе можно описать так:

node_tree struc ;узел дерева

simbol db 0 содержательная часть

l_son dd 0 указатель на старшего (левого) сына

r_son dd 0 указатель на младшего (правого) сына

ends

Рассмотрим на простом примере реализацию основных операций над деревом. Ранее при обсуждении сортировок упоминался двоичный поиск. При этом говорилось, что сам алгоритм совпадает с алгоритмом прохождения пути от вершины двоичного дерева к заданной его вершине. Реализуем этот вид поиска, но уже с использованием действительно двоичного дерева. Для начала построим двоичное дерево, используя произвольный массив чисел.

Работа с массивами

Приемы практической работы с массивами продемонстрируем на примерах выполнения конкретных операций: сортировка массива, поиск в массиве, транспонирование матрицы и др. На примере работы с массивами очень удобно обсуждать особенности реализации этих операций, так как в общем случае элементы массива могут быть не просто скалярами, но и более сложными по структуре данными. Поэтому дальнейшее наше изложение помимо демонстрации приемов работы с массивами в программах на ассемблере будет посвящено рассмотрению возможных подходов к реализации нескольких классов практически важных алгоритмов.

Сеть

Неважно, что кто-то идет неправильно,

возможно, это хорошо выглядит...

Первый закон Скотта (Прикладная Мерфология)

Выше мы уделили достаточно внимания работе с матрицами и списками, и это сделано не случайно. Еще более обобщая понятие списка, мы придем к определению многосвязного списка, для которого характерно наличие произвольного количества указателей на другие элементы списка. Можно говорить, что каждый конкретный элемент входит в такое количество односвязных списков, сколько у него есть указателей. Многосвязный список получается «прошитым» односвяз-ными списками, поэтому такие многосвязные списки называют прошитыми, или плексами. С помощью многосвязных списков можно моделировать такую структуру данных, как сеть или граф. Частный случай сети — дерево. Рассмотрим варианты представления в памяти компьютера этих структур данных.

Сетью называется кортеж G — (V,E), где V — конечное множество вершин, Е -^ конечное множество ребер, соединяющих пары вершин из множества V. Две вершины и и v из множества V называются смежными, если в множестве Е существует ребро (u, v), соединяющее эти вершины. Сеть может быть ориентированной и неориентированной. Это зависит от того, считаются ли ребра (u, v) и (v, u) разными. В практических приложениях часто ребрам приписываются веса, то есть некоторые численные значения. В этом случае сеть называется взвешенной. Для каждой вершины v в сети есть множество смежных вершин, то есть таких вершин Uj (i = l..n), для которых существуют ребра (v, и:). Это далеко не все определения, касающиеся сети, но для нашего изложения их достаточно, так как его цель — иллюстрация средств ассемблера для работы с различными структурами данных. Поэтому рассмотрим варианты представления сетей в памяти компьютера в виде, пригодном для обработки. Какой из этих вариантов лучше, зависит от конкретной задачи. Мы также не будем проводить оценку эффективности того или иного вида представления.

Матрица смежности. Сеть, имеющую М вершин, можно представить в виде матрицы размерностью МхМ. При условии, что вершины помечены v,, v2,..., vm, значение матрицы ау = 1 говорит о существовании ребра между вершинами v, и v,. Иначе говоря, эти вершины являются смежными. Для ориентированной сети матрица смежности будет симметричной.

Матрица инцидентности. В основе этого представления также лежит матрица, но строки в ней соответствуют вершинам, а столбцы — ребрам (Рисунок 2.15). Из рисунка видно, что каждый столбец содержит две единицы в строках, причем одинаковых столбцов в матрице нет.

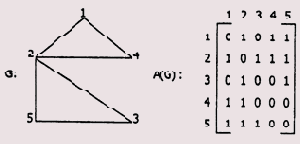
Рисунок 2.15. Представление сети матрицей инцидентности

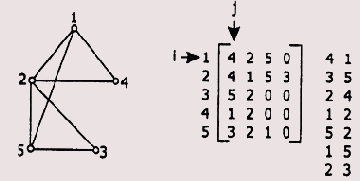
Рисунок 2.16. Представление сети векторами смежности

Векторы смежности. Этот вариант представления также матричный (Рисунок 2.16). Все вершины пронумерованы. Каждой вершине соответствует строка матрицы, в которой перечислены номера вершин, смежных с данной.

В качестве примера рассмотрим фрагмент сканера для распознавания вещественных чисел в директивах ассемблера dd, dq, dt. Правило описания этих чисел в виде синтаксической диаграммы приведено в уроке 19 «Архитектура и программирование сопроцессора» учебника. Ему соответствует показанное ниже регулярное выражение и детерминированный конечный автомат (Рисунок 2.17):

(+|-)dd*.dd*e(+|-)dd*

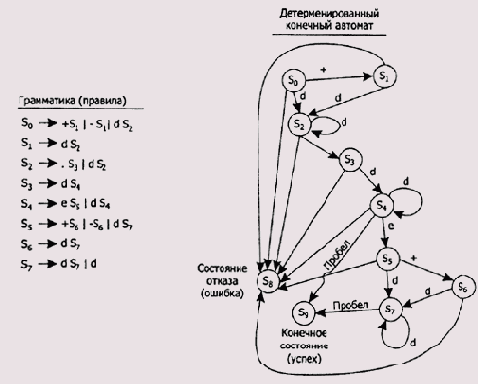
Рисунок 2.17. Грамматика языка описания вещественных чисел в директиве dd и соответствующий ей детерминированный конечный автомат

Программа будет состоять из двух частей:

построение списка — здесь выполняется построение многосвязного списка по заданному регулярному выражению;

обработка входной строки на предмет выяснения того, является ли она правильной записью вещественного числа в директивах ассемблера dd, dq, dt.

При выполнении первого пункта возникает проблема — как задавать элемент многосвязного списка, если в общем случае различные элементы списка могут иметь разное количество связей? Как показано на рисунке, различные состояния имеют разное количество связей. Можно предложить разные подходы к выбору программной реализации этих связей. Выберем следующий. Организуем все исходящие связи каждого конкретного элемента в односвязный список. В этом случае многосвязный список будет содержать элементы двух типов:

описывающие состояния автомата — они организованы в двусвязный список;

описывающие ссылки или переходы от данного состояния к другим состояниям в зависимости от очередного входного символа — эти ссылки организованы в виде односвязных списков для каждого из состояний.

В случае нелинейной организации двусвязного списка его построение таит ряд проблем. Часть из них снимается при статическом способе построения списка, который для конечных автоматов является наилучшим. При необходимости, используя приведенные ниже структуры, читатель может самостоятельно описать такой список в своем сегменте данных. Далее мы займемся динамическим, более сложным вариантом организации нелинейного списка, реализующим конечный автомат. Напомним, что его задачей является распознавание лексемы — описания шестнадцатеричного числа в директивах ассемблера dd, dq, dt. Для построения нелинейного многосвязного списка разработаем ряд макрокоманд. С их помощью построение проводится в два этапа:

создание двусвязного списка состояний конечного автомата;

создание односвязных списков переходов.

В приведенной ниже программе двусвязный список состояний конечного автомата строится сразу. Далее для каждого состояния, в котором может находиться автомат, строятся односвязные списки переходов. По мере своего создания односвязные списки переходов подсоединяются к соответствующим элементам двусвязного списка состояний конечного автомата. В конце программы производится распознавание строки string на предмет ее принадлежности к множеству строк, описываемых приведенным выше регулярным выражением для вещественного числа.

;но при необходимости можно создать и доп. кучу с помощью HeapCreate :HANDLE GetProcessHeap (VOID);

call GetProcessHeap

mov Hand_Head.eax :сохраняем дескриптор .запрашиваем и инициализируем блоки памяти из кучи:

xorebx.ebx :здесь будут указатели на предыдущ. элементы

xorecx.ecx ;dl - номер элемента состояния (двоичный) rept N_state

push ecx :LPVOID HeapAlloc(HANDLE hHeap. DWORD dwFlags, DWORD dwBytes);

push type descr ;размер структуры

push 0 :флаги не задаем

push HandJHead ;описатель кучи

call HeapAlloc

mov [eax].prev_state.ebx запоминаем адрес предыдущ. (if ebx=0. то это первый)

movebx.eax запоминаем адрес текущего в ebx

raov [eax].current_state,eax (И в descr.current_state

pop ecx

mov [eax].id_state_state,cl

inc cl endm

указатель на последний элемент списка состояний в поле-указатель на начало списка head

mov head.ebx .восстанавливаем регистры

pop ebx

pop eax endm

Синтаксический анализ

После того как лексемы входного потока распознаны, транслятору необходимо удостовериться, что вся их совокупность является синтаксически правильной. Вопрос: зачем? Заглянем немного вперед и задумаемся о том, каким образом производится генерация кода. Если рассматривать этот вопрос схематично, то можно утверждать, что для каждого нетерминала грамматики существует некий шаблон кода, который подставляется в определенное место выходного кода. Настройка этого шаблона производится значениями лексем, распознанными сканером. Извлечь эту информацию можно, если соответствующая конструкция в исходном коде синтаксически правильна. В конечном итоге мы должны доказать, что вся программа синтаксически правильна.

Цель синтаксического анализа — доказать существование дерева грамматического разбора в контекстно-свободной грамматике G для входной цепочки s, состоящей из терминальных символов.

Существует много различных методов синтаксического анализа программ. Но главное понимать, что все они неявно стремятся доказать одно и тоже — существование синтаксического дерева для транслируемой программы. Ведь применительно к нашей грамматике не может блок описания переменных следовать где-то в середине или конце программы, за операторами, которые эти переменные используют. Кстати, посмотрите сейчас еще раз на правило грамматики, соответствующее начальному символу языка. В этом правиле определена общая структура программы и в ней видно место блока описаний переменных. Вместо списка стоит нетерминал. Можно нарисовать воображаемую дугу к правилу грамматики, соответствующему нетерминалу блока описания переменных, и т. д. То есть мы действительно начали строить грамматическое дерево. И если нам удастся его построить для данной программы, то последняя действительно синтаксически правильна. Если на каком-то шаге построения этого дерева у нас случится ошибка, допустим в том же блоке описания переменных программы вместо идентификатора будет стоять целое число, то дерево мы построить не сможем. То есть программа синтаксически неправильная. Можно формировать соответствующее диагностическое сообщение.

Таким образом, можно утверждать, что если возможно построение дерева трансляции для данного входного потока, то он синтаксически правилен. Понятно, что для другого текста программы дерево трансляции будет другое, но в лю-

бом случае листьями этого дерева будут лексемы программы, а корнем — начальный символ языка. Причем если совершить обход листьев дерева слева направо, то получим вытянутый в строку текст нашей программы.

Если судить по рисунку, то программа синтаксически правильная. Но каким бразом выясняет этот факт транслятор? Как отмечено выше, существует несколько методов выполнения синтаксического анализа. Все они делятся на два класса в зависимости от того, как они движутся по дереву трансляции во время разбора — сверху вниз или снизу вверх. Алгоритмы «сверху вниз» стремятся построить дерево трансляции начиная вывод от начального символа языка к анализируемой цепочке. И наоборот, алгоритмы «снизу вверх» строят дерево трансляции от анализируемой цепочки терминалов к начальному символу языка. Важно подчеркнуть, что на самом деле никакого дерева в памяти нет и не строится. Как показано выше, его структура заложена в правилах грамматики. Используя алгоритм конкретного метода синтаксического разбора и представленные определенным образом в памяти правила грамматики, мы и производим движение по воображаемому дереву трансляции.

На практике не исключены случаи комбинированного применения восходящих и нисходящих методов синтаксического анализа. Например, арифметические выражения удобно разбирать с помощью восходящих методов, а общий разбор программы делать нисходящими методами. В большинстве случаев достаточно одного универсального метода — метода рекурсивного спуска. Для краткости будем называть синтаксический анализатор распознавателем.

Метод рекурсивного спуска

Главное свойство нисходящих методов — их целенаправленность. Метод рекурсивного спуска — наиболее яркий и простой представитель этих методов. Основ ной его недостаток — сильная зависимость от конкретного языка. Программа распознавателя рекурсивного спуска представляет собой, по сути, набор рекурсивных процедур — по одной для каждого из нетерминалов грамматики. Первой получает управление процедура, соответствующая нетерминалу — начальному символу языка. Эта процедура уже знает, что она должна делать. Если первый символ в этом правиле — терминал, то процедура знает об этом и ждет его. Это ожидание заключается в том, что процедура сравнивает код терминала, который должен быть первым, согласно правилу, с кодом первой лексемы из лексической свертки входной строки. Если они совпадают, то процесс разбора идет дальше. Если они не совпадают, то фиксируется ошибка. Если очередным символом правила должен быть нетерминал, то в этом месте вызывается соответствующая ему процедура. Эта процедура тоже построена исходя из правила грамматики для этого нетерминала, поэтому ее действия также уже предопределены. И так будет продолжаться до тех пор, пока разбор не вернется к первому правилу, то есть управление вернется процедуре, соответствующей правилу грамматики для начального символа языка. В нашем случае последним должен быть проанализирован факт того, что последний символ во входной строке — терминал кон_прог.

При реализации метода рекурсивного спуска в чистом виде возможны сложности. Посмотрим на правила грамматики, подобные следующим:

dec-list => dec | dec-list ; dec

id-list=> ID | id-list . ID

term => factor | term * factor | term div factor

strut-list => stmt | stmt-list ; stmt

Видно, что эти правила леворекурсивны. Например, рассмотрим следующее правило:

id-list => ID | ID-LIST , ID

В этом правиле вторая альтернатива начинается с нетерминала ID-LIST, то есть в процессе разбора при обращении к процедуре, соответствующей этому нетерминалу, получится бесконечный цикл. Ее необходимо устранить. Для этого соответствующие правила подправляются следующим образом:

dec-list => dec | dec-list ; dec id-HSts» ID I {. ID}

stmt-list => stmt | {: stmt} exp => term {+ term | - term}
term => factor {* factor | div factor}

Теперь для принятия решения о дальнейшем пути выполнения рекурсивной процедуры необходимо просматривать один символ вперед. Если он совпадает с тем, что в правиле, то процедура рекурсивно вызывается снова. Если этот символ любой другой, то производится возврат из этой процедуры. Таким образом, процесс написания программы неявно представляет собой строительство дерева разбора начиная от его корня — начального символа языка. То есть это действительно нисходящий метод.

Остается заметить еще одно достоинство метода рекурсивного спуска. Если очередная языковая конструкция распознана, то почему бы сразу в соответствующей рекурсивной процедуре не «навесить» семантику, то есть генерацию кода.

Но метод рекурсивного спуска не всегда применим. В сложных случаях, когда имеется скрытая левая рекурсия, необходимо применять более сложные методы для ее устранения или замены правой рекурсией.

После этого обсуждения мы готовы написать распознаватель, но делать этого не будем, так как цель, достижению которой был посвящен материал данного раздела, достигнута. Все остальное — техника программирования. Остается добавить, что разговор о проблемах трансляции мы продолжим в главе 10.

Сложные структуры данных Сутью

Сложные структуры данных

Сутью искусства программирования обычно

считается умение составлять операции.

Но не менее важно умение составлять данные.

Н. Вирт

Сортировка массивов

Под сортировкой понимается процесс перестановки элементов некоторого множества в порядке убывания или возрастания. Если элементы множества — скаляры, то сортировка ведется относительно их значений. Если элементы множества — структуры, то каждая структура должна иметь поле, относительно которого будет производиться упорядочивание местоположения элементов (то есть сортировка) относительно других элементов-структур множества.

Различают два типа алгоритмов сортировки: сортировку массивов и сортировку файлов. Другое их название — алгоритмы внутренней и внешней сортировки. Разница заключается в местонахождении объектов сортировки: для внутренней сортировки — это оперативная память компьютера, для внешней — файл. В данном разделе будут рассмотрены алгоритмы внутренней сортировки массивов. Алгоритмы внешней сортировки будут рассмотрены в разделе, посвященном работе с файлами.

Существует несколько алгоритмов сортировки массивов, которым следует уделить внимание в контексте проблемы изучения ассемблера. По критерию эффективности алгоритмы сортировки массивов делят на простые и улучшенные. Среди простых методов сортировки, которые также называют сортировками «на том же месте», мы рассмотрим следующие:

сортировка прямым включением;

сортировка прямым выбором;

сортировка прямым обменом.

Улучшенные методы сортировки в нашем изложении будут представлены следующими алгоритмами:

сортировка Шелла;

сортировка с помощью дерева;

быстрая сортировка.

Сортировка прямым включением

Идея сортировки прямым включением (программа prg4_96.asm) заключается в том, что в сортируемой последовательности masi длиной n (i = 0..n - 1) последовательно выбираются элементы начиная со второго (i< 1) и ищутся их местоположения в уже отсортированной левой части последовательности. При этом поиск места включения очередного элемента х в левой части последовательности mas может закончиться двумя ситуациями:

найден элемент последовательности mas, для которого masi<x;

достигнут левый конец отсортированной слева последовательности.

Первая ситуация разрешается тем, что последовательность mas начиная с masi раздвигается в правую сторону и на место masi перемещается х. Во второй ситуации следует сместить всю последовательность вправо и на место mas0 переместить х.

В этом алгоритме для отслеживания условия окончания просмотра влево отсортированной последовательности используется прием «барьера». Суть его в том, что к исходной последовательности слева добавляется фиктивный элемент X. В начале каждого шага просмотра влево отсортированной части массива элемент X устанавливается в значение того элемента, для которого будет осуществляться поиск места вставки.

ПРОГРАММА рrg4_96

//prg4_96 - программа на псевдоязыке сортировки прямым включением //Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений. //Выход: mas[n] - упорядоченная последовательность байтовых двоичных значений. //.---------...----...--.........

ПЕРЕМЕННЫЕ

INT_BYTE n=8: //количество элементов в сортируемом массиве

INT_BYTE mas[n]: //сортируемый массив размерностью п (О..п-l)

INT_BYTE X; //барьер

INT_BYTE i=0: j=0 //индексы

НАЧ_ПРОГ

ДЛЯ 1:-1 ДО п-1 /Л изменяется в диапазоне О..п-l

НАЧ_БЛ0К_1

//присвоение исходных значений для очередного шага

X:=mas[i]: mas[0]:=X; j:=i-l

ПОКА (X<mas[j]) ДЕЛАТЬ НАЧ_БЛОК_2

mas[j+l]:=mas[j]; j:=j-l КОН_БЛ0К_2

mas[j+l]:=X

КОН_БЛОК_1 КОН_ПРОГ

;prg4_96.asm - программа на ассемблере сортировки прямым включением.

.data

mas db 44,55.12.42.94.18.06.67 :задаем массив

n=$-mas

X db 0 :барьер

.code

mov ex.п-1 :цикл по 1

movsi.l :i=2 сус13: присвоение исходных значений для очередного шага

mov al ,mas[si]

movx.al :X: = mas[i]: mas[0]:-X: j:=i-l

push si ;временно сохраним i. теперь J-1 :еще один цикл, который перебирает элементы до барьера x=mas[i] сус12: mov al,mas[si-l]

emp x,al ;сравнить х < mas[j-l]

ja ml :если x > mas[j-l] : если x < mas[j-l]. то

mov al,mas[si-l]

irovmas[si],al

dec si

jmpcycl2 ml: mov al ,x

movmas[si].al

pop si

incsi

loop cyc!3

Этот способ сортировки не очень экономен, хотя логически он выглядит очень естественно.

Сортировка прямым выбором

В алгоритме сортировки прямым выбором (программа prg4_99.asm) на каждом шаге просмотру подвергается несортированная правая часть массива. В ней ищется очередной минимальный элемент. Если он найден, то производится его перемещение на место крайнего левого элемента несортированной правой части массива.

ПРОГРАММА prg4_99

//prg4_99 - программа на псевдоязыке сортировки прямым выбором //Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений. //Выход: mas[n] - упорядоченная последовательность байтовых двоичных значений. // .

ПЕРЕМЕННЫЕ

INT_BYTE n=8; //количество элементов в сортируемом массиве INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-l) INTJYTE X: i=0: j=0: k=0 // i. j, k - индексы НАЧ_ПРОГ

ДЛЯ i:=l ДО n-1 //i изменяется в диапазоне 1..П-1 НАЧ_6ЛОК_1

//присвоение исходных значений для очередного шага k:=i: Х: = raas[i]

ДЛЯ j:-1+l ДО n //j изменяется в диапазоне 1+1..п ЕСЛИ mas[j]<X TO НАЧ_БЛ0К_2

k:=j: x:= mas[j] К0Н_БЛ0К_2

mas[k]:= mas[i]; mas[i]:=X КОН_БЛОК_1 КОН_ПРОГ

;prg4_99.asm - программа на ассемблере сортировки прямым выбором.

.data

masdb 44.55.12,42,94,18.06,67 ;задаем массив

n-$-mas

X db 0

К dw 0

.code

:внешний цикл - по 1

mov сх.л-1

mov si ,0 cycll: push ex

mov k.si :k:=i

mov al ,mas[si]

movx.al ;x:=mas[i]

push si :временно сохраним i - теперь j=I+l

incsi :j=I+l

сложенный цикл - по j

mov al ,n

sub ax.si

mov ex,ax количество повторений внутреннего цикла по j cycl2: mov al ,mas[si]

cmpal ,x

ja ml

mov k.si ;k:=j

moval ,mas[si]

movx.al :x:=mas[k] ml: inc si :j:=j+l

loop cycl2

pop si

mov al ,mas[s1]

movdi Л

mov mas[di],al :mas[k]:=mas[i]

mov al,x

mov mas[si],al :mas[i]:-x

inc si

pop ex

loop cycll

Первый вариант сортировки прямым обменом

Этот метод основан на сравнении и обмене пар соседних элементов до их полного упорядочивания (программа prg4_101.asm). В народе этот метод называется методом пузырьковой сортировки. Действительно, если упорядочиваемую последовательность расположить не слева направо, а сверху вниз («слева» — это «верх»), то визуально каждый шаг сортировки будет напоминать всплытие легких (меньших по значению) пузырьков вверх.

ПРОГРАММА prg4_101

//..

//prg4_101 - программа на псевдоязыке сортировки прямым обменом 1

//Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений.

//Выход: mas[n] - упорядоченная последовательность байтовых двоичных значений.

//....-..

ПЕРЕМЕННЫЕ

INTJ3YTE n=8: //количество элементов в сортируемом массиве INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-l) INTJYTE X: i-0; j-0 // i. j - индексы НАЧ_ПРОГ

ДЛЯ i:=l ДО n-1 //i изменяется в диапазоне L.n-l НАЧ_БЛ0К_1

ДЛЯ j:=n-l ДОВНИЗ i //j изменяется в диапазоне 1+1.,П ЕСЛИ mas[j-l]< mas[j] TO НАЧ_БЛОК_2

x:=mas[j-l]; mas[j-l]:=mas[j]: mas[j]:=X К0Н_БЛ0К_'2 К0Н_БЛ0К_1 КОН_ПРОГ

;prg4_101.asm - программа на ассемблере сортировки прямым выбором 1.

ПОВТОРИТЬ

.data ДЛЯ j:=r ДОВНИЗ 1 //j изменяв!

: задаем массив ЕСЛИ mas[j-l]< mas[j] TO

masdb 44,55.12,42.94.18.06,67 НАЧ^БЛОК_1

n=$-mas x:=mas[j-l]: mas[j-l]:

X db 0 КОН БЛОК 1

ДЛЯ j:-l ДОВНИЗ г //j изменяв"

.code ЕСЛИ mas[j-l]< mas[j] TO

НАЧ_БЛОК_2

;внешний цикл - по 1 x:=mas[j-l]: mas[j-l]:

mov ex, n -1 КОН БЛОК 2

mov si .1 r:=k-l

cycl1: ПОКА (1>г)

push ex КОН_ПРОГ

mov ex n

1 1 1\щ/ V \— Г\ , 1 1 sub ex,si количество повторений внутреннего цикла :prg4 104.asm - программа на аса

push si временно сохраним i - теперь j=n mov si ,n-l

cycl2: :ЕСЛИ mas[j-l]< mas[j] TO .data

mov al ,mas[si-l] :задаем массив

cmpmas[si].al masdb 44.55,12.42.94.18.06.67

ja ml n=$-mas

movx.al :x=mas[j-l] X db 0

mov al ,mas[si] L dw 1

mov mas[si-l],al ;mas[j-l]= mas[j] R dw n

mov al,x k dw n

mov mas[si].al :mas[j]=x

ml: dec si :цикл по j с декрементом n-i раз .code

loop cycl2 ;.... :1:=2: г:=n: k: =n

pop si cycl3: :ДЛЯ j:-r ДОВНИЗ 1

inc si mov si .R : j:=R

pop ex push si

loop cycll sub si.L

;.... mov ex,si количество по

pop si

Второй вариант сортировки прямым обменом

Эту сортировку называют шейкерной (программа prg4_104.asm). Она представляет собой вариант пузырьковой сортировки и предназначена для случая, когда последовательность почти упорядочена. Отличие шейкерной сортировки от пу зырьковой в том, что на каждой итерации меняется направление очередного про хода: слева направо, справа налево.

ПРОГРАММА prg4_104 mov mas[si-l].al :mas[j-

mov al ,x

//prg4_104 - программа на псевдоязыке сортировки прямым обменом 2 (шейкерной) mov mas[si].al ;mas[j]:-x

//Вход: mas[n] - неупорядоченная последовательность байтовых двоичных значений. mov k.si :k:=j

//Выход: mas[n] -упорядоченная последовательность байтовых двоичных значений. ml: dec si :j:=j-l

loop cycll

ПЕРЕМЕННЫЕ mov ax.k

INT BYTE n=8: //количество элементов в сортируемом массиве inc ax

INT BYTE mas[n]: //сортируемый массив размерностью п (О..п-l) mov Lax :L:=k+l

INT BYTE X: 1-0; j=0: г=0: 1=0: k=0 // i. j. г. 1. k - индексы : цикл cycl2 :ДЛЯ j:=l ДОВНИЗ

НАЧ_ПРОГ mov si.L :j:=L

1:=2: r:=n; k:=n mov ax.R

ПОВТОРИТЬ

ДЛЯ j:=r ДОВНИЗ 1 //j изменяется от 1 до г ЕСЛИ mas[j-l]< mas[j] TO НАЧ_БЛОК_1

x:=mas[j-l]: mas[j-l]:=mas[j]: mas[j]:=X: k:=j КОН_БЛОК_1

ДЛЯ j:=l ДОВНИЗ г //j изменяется от г до 1 ЕСЛИ mas[j-l]< mas[j] TO НАЧ_БЛОК_2

x:-mas[j-l]; mas[j-l]:=mas[j]; mas[j]:=X; k:=j К0Н_БЛ0К_2 r:=k-l ПОКА (1>г) КОН_ПРОГ

:prg4_104.asm - программа на ассемблере сортировки прямым выбором 2 (шейкерной).

.data

: задаем массив

masdb 44.55.12.42.94.18.06.67

n=$-mas

X db 0

L dw 1

R dw n

k dw n

.code

;.... :1:=2: r:=n: k:=n

cycl3: :ДЛЯ ДОВНИЗ 1

mov si.R :j:=R

push si

sub si.L

mov ex,si количество повторений цикла cycll

pop si

dec si cycll: :ЕСЛИ mas[j-l]< mas[j] TO

mov al,mas[si-1]

emp al.mas[si]

jna ml

mov al,mas[si-1]

mov x.al ;x:=mas[j-l]

mov al.mas[si]

mov mas[si-l].al :mas[j-l]:=mas[j]

mov a 1, x

mov mas[si].al :mas[j]:=x

mov k.si ;k:=j

ml: dec si :j:=j -1

loop cycll

mov ax.k

inc ax

mov L.ax :L:=k+l : цикл сус12 :ДЛЯ j:-l ДОВНИЗ г

mov si.L :j:=L

mov ax.R

sub ax.L

mov ex.ax количество повторений цикла сус12

cyc12: mov al.mas[si-l] :ЕСЛИ mas[j-l]< mas[j] TO

emp al.mas[si]

jna m2

mov al,mas[si-l]

mov x.al ;x:=mas[j-l]

mov al.mas[si]

mov mas[si-l].al ;mas[j-l]:=mas[j]

mov al .x

mov mas[si].al :mas[j]:=x

mov k.s1 :k:=j

m2: inc si :j:=j+l

loop cycl2

mov ax.k

dec ax

mov R.ax :R:=k-1

emp L.ax ;L>R - ?

jae $+5

jmp cycl3

Улучшение классических методов сортировки

Приведенные выше четыре метода сортировки — базовые. Их обычно рассматривают как основу для последующего обсуждения и совершенствования. Ниже мы рассмотрим несколько усовершенствованных методов сортировки, после чего вы сможете оценить эффективность их всех.

Сортировка Шелла

Приводимый ниже алгоритм сортировки (программа prg4_107.asm) носит имя автора, который предложил его в 1959 году. Суть его состоит в том, что сортировке подвергаются не все подряд элементы последовательности, а только отстоящие друг от друга на определенном расстоянии h. На каждом шаге значение h изменяется, пока не станет (обязательно) равно 1. Важно правильно подобрать значения h для каждого шага. От этого зависит скорость работы алгоритма. В качестве значений h могут быть следующие числовые последовательности: (4, 2, 1), (8, 4, 2, 1) и даже (7, 5, 3, 1). Последовательности чисел можно вычислять аналитически. Так, Кнут предлагает следующие соотношения:

Nk-1 = 3Nk+1, в результате получается последовательность смещений: 1, 4, 13,40,121...

Nk-1, = 2Nk+l, в результате получается последовательность смещений: 1, 3, 7, 15, 31...

Подобное аналитическое получение последовательности смещений дает возможность разрабатывать программу, которая динамически подстраивается под конкретный сортируемый массив.

Отметим, что если h=1, то алгоритм сортировки Шелла вырождается в сортировку прямыми включениями.

Существует несколько вариантов алгоритма данной сортировки. Вариант, рассмотренный ниже, основывается на алгоритме, предложенном Кнутом.

ПРОГРАММА prg4_107

//prg4_107 - программа на псевдоязыке сортировки Шелла

//Вход: mas_dist=(7,5,3.1) - массив смещений: mas[n] - неупорядоченная

последовательность байтовых двоичных значений. //Выход: mas[n] -упорядоченная последовательность байтовых двоичных значений.

-ПЕРЕМЕННЫЕ

INT_BYTE t=4; //количество элементов в массиве смещений

INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-1)

INT_BYTE mas_dist[t]=(7.5,3,l): // массив смещений размерностью t (O..t-1)

INT_BYTE h=0 //очередное смещение из mas_dist[]

INT_BYTE X: i=0: j-0; s=0 // i. j. s - индексы

НАЧ_ПРОГ

ДЛЯ s:=0 ДО t-1 НАЧ_БЛОК_1

h:=mas_dist[s] ДЛЯ j:4i ДО n-1 НАЧ_БЛ0К_2

i:=j-h: X:=mas[i]

@@d4: ЕСЛИ Х>= mas[i] TO ПЕРЕЙТИ_НА №66 mas[i+h]:=mas[i]: i:=i-h ЕСЛИ 1>0 ТО ЛЕРЕЙТИ__НА @@d4 Ш6: mas[i+h]:=x К0Н_БЛ0К_2 КОН_БЛОК_1 КОН_ПРОГ

:prg4_107.asm - программа на ассемблере сортировки Шелла

.data

: задаем массив

masdb 44,55.12.42.94.18,06,67

n=$-mas

X db 0

:задаем массив расстояний

mas_dist db 7.5.3.1

t=$-mas_dist ;t - количество элементов в массиве расстояний

.code

xorbx.bx :в bx - очередное смещение из mas_dist[] :dl

movcx.t :цикл по t (внешний)

movsi.O :индекс по mas_dist[] (?@d2: push ex

mov bl,mas_dist[si] :в bx - очередное смещение из mas_dist[]

inc si push si :ДЛЯ j:=h ДО n-1

mov di.bx ' ;di - это j :j:=h+l - это неявно для нумерации массива с нуля @@d3: cmpdi.n-1 ;j=<n ?

ja @@ml :конец итерации при очередном mas_dist[]

mov si ,di

sub si.bx :i:=j-h: si - это i

mov al ,mas[di] ;x:=mas[j]

movx.al :x:=mas[j] @@d4: :ЕСЛИ Х>= mas[i] TO ПЕРЕЙТИ_НА №й6

mov al,x

cmpal ,mas[si]

jae@@d6

:d5 - mas[i+h]:=mas[i]: i:=i-h push di push si popdi

adddi.bx :i+h

mov al, mas[si] :mas[i+h]:=mas[i]

movmas[di],al :mas[i+h]:=mas[i] pop di

subsi.bx ;i:=i-h

cmpsi.O ;ЕСЛИ i>0 TO ПЕРЕЙТИ_НА @@d4

jg Ш4

@@d6: ;mas[i+h]:=x

push di push si pop di

adddi.bx ;i+h

mov al .x

movmas[di].al ;mas[i+h]:=x popdi

incdi :j:=j+l

jmp ШЗ @@ml: pop si pop ex

loop Ш2 @@exit:

Сортировка с помощью дерева

Следующий алгоритм (программа prgl0_229.asm) является улучшением сортировки прямым выбором. Автор алгоритма сортировки с помощью дерева — Дж. У. Дж. Уильяме (1964 год). В литературе этот алгоритм носит название «пирамидальной» сортировки. Если обсужденные выше сортировки интуитивно понятны, то алгоритм данной сортировки необходимо пояснить подробнее. Этот алгоритм предназначен для сортировки последовательности чисел, которые являются отображением в памяти дерева специальной структуры — пирамиды. Пирамида — помеченное корневое двоичное дерево заданной высоты h, обладающее тремя свойствами:

каждая конечная вершина имеет высоту h или h-1;

каждая конечная вершина высоты h нажщится слева от любой конечной вершины высоты h-1;

метка любой вершины больше метки любой следующей за ней вершины.

На Рисунок 2.3 изображено несколько деревьев, из которых лишь одно Т4 является пирамидой.

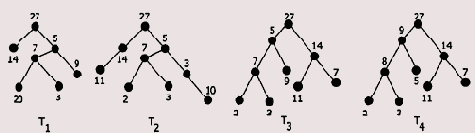
Рисунок 2.3. Примеры деревьев (Т4 — пирамида)

Такая структура пирамид позволяет компактно располагать их в памяти. Например, пирамида, показанная на рисунке, в памяти будет представлена следующим массивом: 27, 9, 14, 8, 5, 11, 7, 2, 3. Оказывается, что такая последовательность чисел легко подвергается сортировке.

Таким образом, сортировка массива в соответствии с алгоритмом пирамидальной сортировки осуществляется в два этапа: на первом этапе массив преобразуется в отображение пирамиды; на втором — осуществляется собственно сортировка. Соответственно нами должны быть разработаны две процедуры для выполнения задач каждого из этих двух этапов.

ПРОЦЕДУРА insert_item_in_tree (i. mas. N) //

//insert_item_in_tree - процедура на псевдоязыке вставки элемента на свое место

в пирамиду //Вход: mas[n] - сформированная не до конца пирамида: 1 - номер добавляемого элемента

в пирамиду из mas[n] (с конца): n - длина пирамиды //Выход:действие - элемент добавлен в пирамиду.

НАЧ_ПРОГ

j:=i @@ml: k:=2*j: h-k+1

ЕСЛИ (1=<N И (mas[j]<mas[k] ИЛИ mas[j]<mas[l]) TO ПЕРЕЙТИ_НА @йп6

ИНАЧЕ ПЕРЕЙТИ_НА @@m2

КОН_ЕСЛИ @@m6: ЕСЛИ tnas[k]>mas[l] TO ПЕРЕЙТИ_НА @@т4

ИНАЧЕ ПЕРЕЙТИ_НА @@тЗ

КОН_ЕСЛИ @@т4: x:=mas[j]

mas[j]:=mas[k]

j:=k

mas[k]:=x ПЕРЕЙТИ_НА (a0ml (а@тЗ: x:=mas[j]

mas[j]:=mas[l]

mas[l]:=x

ПЕРЕЙТИ_НА @@ml*

@@m2: ЕСЛИ (k==n И mas[j]<mas[k]) TO ПЕРЕЙТИ_НА @@m7

ИНАЧЕ ПЕРЕЙТИ_НА @@m8

КОН_ЕСЛИ @@m7: x:=mas[j]

mas[j]:=mas[n]

;m-n/2 - значение, равное половине числа элементов массива mas

push si push ex

movj.si :j\»1 @@m4:

movsi.j :i->si

movax.j :k:=2*j; l:-k+l

shlax.l :j*2

movk.ax : k :=j*2

inc ax

movl.ax :l:»k+l

cmpax.m :l<m

ja @@m2

moval ,raas[si-l] ;ax:-mas[j]

mov di,k

emp al ,mas[di-l]

jna @@m6

inc di

emp al.mas[di-l]

jna @@m6

jmp @@m2

@@m6: ;условие выполнилось:

;2j+l+<M AND (mas[j]<mas[2j] OR mas[j]<mas[2j+l]) :обмен с mas[j]

mov di,k

mov al ,mas[di-1] ;ax:=mas[k]

inc di

emp al,mas[di-l] :mas[k]>mas[l]

jna ШтЗ

mov al ,raas[si-l]

movx.al ;x:=rnas[j]

dec di

mov al ,mas[di-l]

movmas[si-l].al :mas[j]:=mas[k]

movj.di :j:=k

mov al .x

movmas[di-l],al :mas[k]:=x

jmp @?m4

:@@m3: x:=mas[j] ;ПЕРЕЙТИ_НА @@ml №m3: :mas[k] =< mas[l]

mov al,mas[si-l]

movx.al :x:=mas[j]

mov al,mas[di-l]

movmas[si-l].al ;mas[j]:=mas[l]

movj.di :j:=l

mov al ,x

movmas[di-l].al ;mas[l]:=x

jmp @@m4 Шт2: ; условие не выполнилось: 2j+l+<M AND (mas[j]<mas[2j] OR mas[j]<mas[2j+l])

mov ax.k

emp ax.m

Нахождение медианы

Медиана - элемент последовательности, значение которго не больше значений одной половины этой последовательности. Например, медианой последовательности чисел 38 7 5 90 65 8 74 43 2 является 38.

оответствующая отсортированная последовательность будет выглядеть так: 2 5 7 8 38 43 65 74 90.

Задачу нахождения медианы можно решить просто — предварительно отсортировать исходный массив и выбрать средний элемент. Но К. Хоор предлагает метод, который решает задачу нахождения медианы быстрее и соответственно может рассматриваться как вспомогательный для реализации других задач. Достоинство метода К. Хоора заключается в том, что с его помощью можно эффективно находить не только медиану, но и значение k-го по величине элемента последовательности. Например, третьим по величине элементом приведенной выше последовательности будет 7.

Значение k-го элемента массива определяется по формуле k=n/2, где п — длина исходной последовательности чисел.

Ниже приведена программа prg4_123.asm, которая находит элемент-медиану массива. Аналогичную функцию выполняет и процедура median, но процедура отличается тем, что ее можно вызывать динамически во время работы программы, в которой она используется.

ПРОГРАММА prg4_123

//

//prg4_123 - программа на псевдоязыке нахождения k- го по величине элемента массива mas

длиною п. Для нахождения медианы к=п/2. //Вход: mas[n] - неупорядоченная последовательность двоичных значений: к - номер

искомого по величине элемента mas[n]. //Выход: х - значение к-го по величине элемента последовательности mas[n].

// .....

ПЕРЕМЕННЫЕ

INT_BYTE n: ;длина mas[n]

INT_BYTE mas[n]: //сортируемый массив размерностью n (О..n-l)

INTJYTE X:W;i=0: j=0; 1=0; г=0 // j: 1; г - индексы

НАЧПРОГ

1:=1: г:=п ПОКА 1<г ДЕЛАТЬ НАЧ_БЛОК_1 х:=а[к]: 1:=1: j:=r ПОВТОРИТЬ

ПОКА a[i]<x ДЕЛАТЬ i:=i+l ПОКА х< a[j] ДЕЛАТЬ j:=j-l ЕСЛИ i<j TO НАЧ_БЛ0К_2

w:=a[i]: а[1]:-аШ; a[j]:=w i:=i+l: j:=j-l К0Н_БЛ0К_2 ПОКА (i>j) ЕСЛИ j<k TO 1:=I ЕСЛИ k<i T0 r:=j КОН_БЛОК_1 КОН_ПРОГ

;prg4_123 - программа на ассемблере нахождения k-го по величине элемента массива mas длиною п. Для нахождения медианы к=п/2.

.data

jge $+6

movR.di :R<-J :цикл(1)конец jmp @@m8

Быстрая сортировка

Последний рассматриваемый нами алгоритм (программа prglO_223.asm) является улучшенным вариантом сортировки прямым обменом. Этот метод разработан К. Хоором в 1962 году и назван им «быстрой сортировкой». Эффективность быстрой сортировки зависит от степени упорядоченности исходного массива. Для сильно неупорядоченных массивов — это один из лучших методов сортировки. В худшем случае, когда исходный массив почти упорядочен, его быстрая сортировка по эффективности не намного лучше сортировки прямым обменом.

Идея метода быстрой сортировки состоит в следующем. Первоначально среди элементов сортируемого массива mas[l. .n] выбирается один mas[k], относительно которого выполняется переупорядочивание остальных элементов по принципу — элементы mas[i]<mas[k] (i=0. .n-1) помещаются в левую часть mas; элементы mas[i]>mas[k] (i=0. .n-1) помещаются в правую часть mas. Далее процедура повторяется в полученных левой и правой подпоследовательностях и т. д. В конечном итоге исходный массив будет правильно отсортирован. В идеальном случае элемент mas[k] должен являться медианой последовательности, то есть элементом последовательности, значение которого не больше значений одной части и не меньше значений оставшейся части этой последовательности. Нахождению медианы было посвящено обсуждение программ предыдущего раздела. В следующей программе элементом mas[k] является самый левый элемент подпоследовательности.

ПРОГРАММА prg27_136

//prg27_136 (по Кнуту) - программа на псевдоязыке «быстрой сортировки» массива. //Вход: mas[n] - неупорядоченная последовательность двоичных значений длиной п. //Выход: mas[n] -упорядоченная последовательность двоичных значений длиной n.

ПЕРЕМЕННЫЕ

INTJYTE n: //длина mas[n]

INT_BYTE mas[n]; //сортируемый массив размерностью п (О..п-1)

INTJYTE К; TEMP: i=0; j=0: 1=0: г=0; // i. j. 1. г - индексы

INT_WORD M=l //длина подпоследовательности, для которой производится сортировка методом

прямых включений //для отладки возьмем М=1 НАЧ_ПРОГ

ЕСЛИ M<N TO ПЕРЕЙТИ_НА q9

1 :-1: г:=п

ВКЛЮЧИТЬ_В_СТЕК (Offffh) //Offffh - признак пустого стека q2: i :-l: j:-r+l: k:=mas[l] q3: ЕСЛИ i=<j-l TO ПЕРЕЙТИ_НА qq3

ПЕРЕЙТИ_НА q4 //итерация прекращена qq3: i:=i+l

ЕСЛИ mas[i]<K TO ПЕРЕЙТИ_НА q3 q4: j:-j-l

ЕСЛИ j<1 TO ПЕРЕЙТИ_НА q5

ЕСЛИ K<mas[j] TO ПЕРЕЙТИ_НА q4

ЕСЛИ j>i TO ПЕРЕЙТИ_НА q6

Iq2: ;1:-1: j:-r+l: k:-nas[l] movsi.L ;i(si):=L mov di . R incdi ;j(di):=R+l xor ax.ax mov al ,mas[si] mov k.al

q3: :ЕСЛИ 1-sj-l TO ПЕРЕЙТИ_НА qq3 inc si ;i:=i+l cmp si.di :i=<j jleqq3

dec si :сохраняем i=<j jmp q4 :ПЕРЕЙТИ_НА д4//итерация прекращена qq3: moval.k ;i:=i+l

cmpmas[si].al :ЕСЛИ mas[i]<K TO ПЕРЕЙТИ_НА q3

jb q3

q4: decdi ;j:=j-l cmpdi.si :j>=i-l jb q5 mov al ,k :ЕСЛИ K<mas[j] TO ПЕРЕЙТИ_НА q4

cmp al ,mas[di]

»jb q4 q5: ;ЕСЛИ j>i TO ПЕРЕЙТИ_НА q6 cmpdi.si :j=<i ??? J9 q6 movbx.L ://обмен mas[l]:= mas[j] mov dl ,mas[bx] xchg mas[di].dl xchg mas[bx].dl jmpq7 :ПЕРЕЙТИ_НА q7 q6: mov dl.masCsi] ; mas[i]<-> mas[j] xchg mas[di].dl xchg mas[si].dl jmpq3 ;ПЕРЕЙТИ_НА q3 q7: ;ЕСЛИ r-j>j-l>M TO mov ax,г

subax.di ;r-j->ax mov bx.di

subbx.l :j-l->bx cmpax.bx :r-j>j-l ??? jl q7_m4

cmpbx.M ;j-l>M ??? jleq7_m3 ;1, r-j>j-l>M - в стек (j+l.r); r:=j-l; перейти на шаг q2

mov ax.di inc ax push ax

(push г mov r.di dec г :г:=j -1 q7_m4: ;r-j>M ??? cmp ax.M jg q7_m2 cmp bx. M

jleq8 ;4. j-l>M>r-j - r:=j-l: перейти на шаг q2

mov r.di

dec г

jmpq2 q7_m3: cmpax.M

jleq8 ;3. r-j>M>j-l - l:=j+l: перейти на шаг q2

mov 1,di

inc 1

jmpq2 q7_m2: :2. j-l>r-j>M - в стек (l.j-1); l:=j+l; перейти на шаг q2

push 1

mov ax.di

inc ax

push ax

mov 1 ,di

inc 1

jmpq2 q8: извлекаем из стека очередную пару (l.r)

pop г

cmpr.Offffh :ЕСЛИ r<>0ffffh TO ПЕРЕЙТИ_НА q2

je q9

pop!

jmpq2 q9: ;сортировка методом пряных включений - при М=1 этот шаг можно опустить (что и сделано

для экономии места)

Обратите внимание на каскад сравнений шага q7, целью которых является проверка выполнения следующих неравенств:

r-j>=j-1>M — в стек (j+l,r); r:-j-1; перейти на шаг q2;

j-1>r-j>M — в стек (1, j-1); I :=j+1; перейти на шаг q2;

r-j>M>j-l — 1 :=j+1; перейти на шаг q2;

j-1>M>r-j — г:=j-1; перейти на шаг q2.

Проверка этих неравенств реализуется в виде попарных сравнений, последовательность которых выглядит так, как показано на Рисунок 2.4.

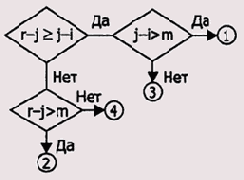
Рисунок 2.4. Последовательность сравнений шага q7

За подробностями алгоритма можно обратиться к тому 3 «Сортировка и поиск» книги Кнута .

Сушествует другой вариант алгоритма этой сортировки — у Вирта в книге «Алгоритмы + структуры данных - программы» [4]. Но у него используется понятие медианы последовательности. Задачу нахождения медианы мы рассматривали выше. Эта задача интересна еще и тем, что она, по сути, является одной из задач поиска, рассмотрению которых посвящен следующий раздел.

Создание односвязного списка переходов для состояния конечного автомата

Также опишем структуру элемента списка переходов и макрокоманду для создания этого элемента. Особенность в том, что в отличие от списка состояний макрокоманда строит не весь список, а только один его элемент. Другая особенность в том, что указатель на полученный односвязный список является ссылкой на последний выделенный элемент списка и именно к этому элементу осуществляется привязка элемента состояния к своему списку переходов, что на самом деле особого значения не имеет.

item_l1st_cross struc ;элемент списка переходов

simbol db 0 :входной символ, при котором автомат переходит

:в состояние ниже (поля id_state_cross и nextjtem) id_state_crossdb 0 идентификатор состояния в списке состояний,

:в которое производится переход

point_state dd 0 ;адрес элемента состояния, в которое производится переход next_item dd 0 :адрес следующего элемента в списке переходов для этого состояния

create_item_cross macro sim:REQ.state:REQ.descr:REQ.head:REQ. Hand_Head:REQ

local ml,@@cycl.exit_m

:создание элемента списка переходов для определенного состояния

:вход:

;регистр ЕВХ - адрес предыдущего (для поля descr.nextjtern),

.-Для первого должен быть равен нулю

:sim - символ ASCII, при поступлении которого производится переход в состояние state

:descr - имя структуры-элемента списка переходов

:state - номер состояния, в которое производится переход

;(если двузначное, то в скобках <>)

:head - имя переменной для хранения указателя на конец списка состояний

;Hand_Head - дескриптор кучи процесса по умолчанию

: выход:

регистр ЕВХ - адрес созданного элемента списка переходов

:флаг cf=l - ошибка: нет такого состояния

сохраняем регистры

push eax

:запрашиваем и инициализируем блок памяти из кучи: :LPVOID HeapAlloc(HANDLE hHeap. DWORD dwFlags. DWORD dwBytes); push type descr ;размер структуры push 0 -.флаги не задаем

push Hand_Head ;описатель кучи call HeapAlloc

mov [eax].next_item.ebx :адрес предыдущего movebx.eax запоминаем адрес текущего

mov [eax].simbol,"&sim" инициализируем поле simbol текущего элемента mov [eax].id_state_cross.state ;номер состояния в поле descr.id_state_cross :теперь нужно определить адрес элемента в списке состояний state для выполнения дальнейших переходов и инициализации поля point_state push ebx mov ebx.head clc

(a@cycl :cmp [ebx].id_state_state,state je ml jc exit_m

mov ebx,[ebx].prev_state ;адрес предыдущего состояния в списке состояний cmpebx.O :последний элемент?

jne @@cycl stc

jmp @@cycl ml: :нашли!

mov [eax].poi nt_state,ebx exitjn: восстанавливаем регистры pop ebx pop eax endm

Далее приведена вспомогательная макрокоманда, которая по номеру состоя-ия определяет адрес соответствующего элемента в списке состояний. def_point_item_state macro N_state:REQ,head:REQ local @(acy,@@ml сохраняем регистры :вход:

:N_state - номер состояния

:head - имя ячейки, где хранится указатель на список состояний :выход: регистр ЕВХ - адрес элемента в списке состояний

mov eax.head

@@су: cmp [eax].id_state_state,N_state :ищем ... je @@ml ;нашли?

moveax,[eax].prev_state ;адрес следующего состояния cmp eax. О последний элемент? jne @@cy

stc ;cf=l если состояния с таким номером не существует

jmp @@су

@@ml: :нашли!

endm

Собственно программа prg02_ll.asm, выполняющая построение и инициализацию конечного автомата для распознавания лексемы вещественного числа в директивах dd, dq и dt, достаточно велика.

Список

Если у веревки есть один конец,

значит, у нее должен быть и другой.

Закон Микша (Прикладная Мерфология)

В общем случае под списком понимается линейно упорядоченная последовательность элементов данных, каждый из которых представляет собой совокупность одних и тех же полей. Упорядоченность элементов данных может быть двоякой:

элементы списка располагаются последовательно как в структуре представления, так и в структуре хранения — список такого типа называется последовательным;

порядок следования элементов определяется с помощью специальных указателей, которые расположены в самих элементах и определяют их соседей справа и/или слева — подобные списки называются связными.

Способы распределения памяти

Прежде чем приступить к рассмотрению того, каким образом поддерживается работа с различными структурами данных на ассемблере, необходимо определиться с тем, как будет решаться проблема распределения памяти. Это важный момент, так как фон-неймановская архитектура современных машин предполагает, что любые данные, обрабатываемые программой, располагаются в памяти. Традиционно в любом языке программирования высокого уровня существуют два способа распределения памяти для переменных и постоянных данных — статический и динамический. Соответственно данные будем называть статическими и динамическими объектами данных. В ассемблере в силу его специфики явно присутствует возможность только статического распределения памяти с помощью директив резервирования и инициализации памяти в сегменте данных. Статические объекты данных занимают отведенную им память на все время работы программы. До сих пор при написании ассемблерных программ мы использовали именно статическое распределение памяти. Недостаток этого типа памяти очевиден — если объект данных занимает большую область памяти и имеет малый период жизни, то выделять память на все время работы программы неразумно. Гораздо эффективнее в таких случаях иметь возможность для временного выделения памяти объекту данных на время его жизни. В этом разделе мы уделим все внимание проблеме динамического распределения памяти в программах на ассемблере.

Динамическими объектами данных называются объекты данных, обладающие двумя особенностями:

распределение/освобождение памяти для объекта данных производится по явному запросу программы;

доступ к динамическим объектам данных производится не по их именам, а посредством указателей, содержащих ссылку (адрес) на созданный динамический объект.

Существует и третья особенность, о которой, возможно, не подозревают программирующие на языках высокого уровня, — технология выделения памяти для динамических объектов данных. Эта технология напрямую зависит от операционной среды, для которой разрабатывается программа. Так, в MS DOS динамическое выделение памяти во время работы приложения осуществляется с помощью двух функций прерывания int 21h-48h (выделение блока памяти) и 49h (освобождение блока памяти). Единицей выделения памяти при этом является параграф (16-байтный блок памяти). С точки зрения современного программирования — это примитивно и не очень интересно. Гораздо большими возможностями обладает наиболее распространенная в настоящее время операционная система Windows.

В Windows существует несколько механизмов динамического выделения памяти:

виртуальная память;

кучи;

отображаемые в память файлы.

Пример использования последнего из перечисленных механизмов был приведен в уроке 20 «ММХ-технология микропроцессоров Intel» учебника. Также отображаемые в память файлы рассматриваются в главе 7 этой книги, посвященной работе с файлами. Для нашего изложения представляют интерес, хотя и в разной степени, первые два механизма.

Стек

Стек — последовательный список, в котором все включения и исключения элементов производятся на одном его конце — по принципу LIFO (Last In First Out — последним — пришел первым ушел). Для стека определены следующие операции:

создание стека;

включение элемента в стек;

исключение элемента из стека;

очистка стека;

проверка объема стека (числа элементов в стеке);

удаление стека.

Создание стека должно сопровождаться инициализацией специального дескриптора стека, который может содержать следующие поля: имя стека, адреса нижней и верхней границ стека, указатель на вершину стека.

Иллюстрацию организации и работы стека произведем на примере задачи, анализирующей правильность согласования скобок в некотором тексте. Причем условимся, что скобки могут быть нескольких видов: (), {}, [], <>. Программа реализована в виде приложения Win32 с использованием функций API Win32 для работы с кучей (из нее выделяется память для стека).

mov ecx,l_string

lea ebx.string

jmp cycl

e_xit: jmp exit cycl: jcxz e_xit

cmp byte ptr [ebx]."("

je m_push

cmp byte ptr [ebx],"["

je m_push

cmp byte ptr [ebx],"{"

je m_push

cmp byte ptr [ebx]."<"

je m_push

cmp byte ptr [ebx],")"

jneml извлекаем элемент из вершины стека и анализируем его

TestEmptyStk char_stk.mes_error

pop_stkchar_stk.<offset temp>

cmp temp." ("

jne mes_error

jmp r_next ml: cmp byte ptr [ebx],"]"

jnem2 извлекаем элемент из вершины стека и анализируем его

TestEmptyStk char_stk.mes_error

pop_stkchar_stk.<offset temp>

cmp temp," ["

jnemes_error

jmp r_next m2: cmp byte ptr [ebx],"}"

jnem3 ¦.извлекаем элемент из вершины стека и анализируем его

TestEmptyStk char_stk.mes_err6r

pop_stkchar_stk,<offset temp>

cmp temp."{"

jne mes_error

jmp r_next m3: cmp byte ptr [ebx],">"

jne rjiext извлекаем элемент из вершины стека и анализируем его

TestEmptyStk char_stk.mes_error

pop_stkchar_stk.<offset temp>

cmp temp,"<"

jne mes__error

jmp r_next m_push: включение скобки в стек

pushstk char_stk.ebx r_next:add ebx,char_stk.si ze_i tern

dec ecx

jmp cycl mes_error: :вывод на экран сообщения об ошибке mes_e

jmp exitexit

exit:

определяем стек на пустоту

pop_stkchar_stk,<offset temp> jncmes_error :стек не пуст :вывод на экран сообщения mes_ok

exit_exit: :выход из приложения

delete_stk char_stk :удаляем блок памяти со стеком

Код, выполняющий работу со стеком, оформлен в виде макрокоманд. При необходимости код можно сделать еще более гибким. Для этого нужно использовать функцию API Win32 HeapReAl 1 ос, которая изменяет размер выделенного блока в сторону его увеличения или уменьшения. В принципе, полезной может оказаться операция определения объема стека, то есть количества элементов в нем. Попробуйте реализовать ее самостоятельно.

Структура

Чтобы правильно использовать машину, важно

добиться хорошего понимания структурных отношений,

существующих между данными, способов представления

таких структур в машине и методов работы с ними.

Д. Кнут

Структура (запись) — конечное упорядоченное множество элементов, в общем случае имеющих различный тип. Элементы, входящие в состав структуры, называют полями структуры. Каждое поле структуры имеет имя, по которому производится обращение к содержимому поля. Пример структуры — совокупность сведений о некотором человеке: номер ИНН, фамилия, имя, отчество, дата рождения, место работы, трудовой стаж и т. п. Подробно порядок описания структур и некоторые приемы работы с ними описаны в учебнике. Поэтому мы, чтобы не повторяться, рассмотрим те практически важные моменты, которые были упущены в учебнике: вложенность структур; использование структур для моделирования таблиц и организация работы с ними.

Связные списки

Связный список — набор элементов, каждый из которых структурно состоит из двух частей — содержательной и связующей. Содержательная часть представляет собой собственно данные или указатель на область памяти, где эти данные

содержатся. Связующая часть предназначена для связи элементов в списке и определяет очередность их следования. Благодаря связующей части в каждом из элементов становятся возможными «путешествия» по списку путем последовательных переходов от одного элемента к другому.

В отличие от последовательного списка связный список относится к динамическим структурам данных. Для них характерны непредсказуемость в числе элементов, которое может быть нулевым, а может и ограничиваться объемом доступной памяти. Другая характеристика связного списка — необязательная физическая смежность элементов в памяти.

Относительно связующей части различают следующие типы связных списков.

Односвязный список — список, начало которого определяется указателем начала, а каждый элемент списка содержит указатель на следующий элемент. Последний элемент должен содержать признак конца списка или указатель на первый элемент списка. В последнем случае мы имеем одно-связный кольцевой список. Преимущество последнего состоит в том, что просмотр всех элементов списка можно начинать с любого элемента, а не только с головы. Более того, в случае кольцевого односвязного списка указателем его начала может быть любой элемент списка. Этот вид списка всегда линейный, так как однозначно задает порядок своего просмотра.

Двусвязный список — список, связующая часть которого состоит из двух указателей — на предыдущий и последующий элементы. Начало и конец списка определяются отдельными указателями. Последние элементы дву-связного списка в каждом из направлений просмотра содержат признаки конца. Если замкнуть эти указатели друг на друга, то мы получим кольцевой двусвязный список. В этом случае потребность в указателе конца списка отпадает. Этот вид списка может быть как линейным (иметь одинаковый порядок просмотра в обоих направлениях), так и нелинейным (второй указатель каждого элемента списка задает порядок просмотра, который не является обратным порядку, устанавливаемому первым указателем).

Многосвязный список — список, связующая часть элементов которого в общем случае содержит произвольное количество указателей. В этом виде списка каждый элемент входит в такое количество односвязных списков, сколько он имеет в себе полей связи.

В общем случае для связанных списков определены следующие операции:

создание связного списка;

включение элемента в связный список, в том числе и после (перед) определенным элементом;

доступ к определенному элементу связного списка (поиск в списке);

исключение элемента из связного списка;

упорядочение (перестройка) связного списка;

очистка связного списка;

проверка объема связного списка (числа элементов в связном списке);

объединение нескольких списков в один;

разбиение одного списка на несколько;

копирование списка;

удаление связного списка.

Связные списки очень важны для представления различных сетевых структур, в частности деревьев, что и будет рассмотрено нами чуть ниже. Пока же рассмотрим работу с некоторыми из обозначенных нами типов связных списков на практических примерах.

Транспонирование прямоугольной матрицы

Приемы работы с массивами размерностью больше 1 удобно рассматривать на типовой задаче, например, такой как транспонирование матрицы.

Суть задачи транспонирования матрицы А = {аij} заключается в замене строк столбцами и столбцов строками в соответствии с формулой а 'ij= аij, где а 'ij — элементы транспонированной матрицы А' = {аij}. Максимальная величина индексов i и j задается константами m (количество строк) и т (количество столбцов), соответственно диапазон их значений составляет: i = 0..m-1, j ~ 0..n-1. Элементы матрицы задаются статически — в сегменте данных.

Выше уже отмечалось то, каким образом производится локализация в памяти элемента многомерного массива исходя из его логического номера при условии, что размерность элементов — 1 байт. Локализация элемента матрицы А относительно базового адреса производится по формуле:

аij = n*i+j. (2.1)

Соответствующий элемент в транспонируемой матрице будет расположен по адресу:

A'ij-m*i+j. (2.2)

Например, рассмотрим матрицу 3x4:

02h 04h 06h 08h

16h 24h 38h 45h

47h 48h 57h 56h

Эта матрица в памяти будет выглядеть так:

02h. 04h, 06h. 08h. 16h. 24h. 38h. 45h. 47h. 48h, 57h. 56h

Транспонированный вариант матрицы:

02h 16h 47h

04h 24h 48h

06h 38h 57h

08h 45h 56h

Транспонированный вариант матрицы в памяти будет выглядеть следующим образом:

02h. 16h. 47h. 04h. 24h. 48h. 06h. 38h, 57h. 08h. 45h. 56h

Для решения задачи «в лоб» по формулам 1 и 2 требуется выделять в памяти область для хранения транспонированной матрицы, совпадающую по размеру с исходной.

;prg29_102.asm - программа на ассемблере транспонирования матрицы.

:Вход: mas[n] - матрица mxn.

:Выход: _mas[n] - транспонированная матрица nxm.

.data

m dw 3 : i =0.. 2

n dw 4 ;j=0..3

:задаем матрицу 3x4 (mxn):

mas db 02h.04h.06h.08h.l6h.24h,38h.45h.47h,48h.57h,56h

s_mas=$-mas

_mas db sjnas dup (Offh)

temp db 0

'code'

mov cx.m

xorsi.si :i:=0 ml: push ex :цикл по i

xordiidi ;J:-0

локализуем masij по формуле: masij=n*i+j m2: mov ax.n

mul si предполагаем, что результат в рамках ах

add ax.di : n*i+j

mov bx.ax

mov al ,mas[bx]

movtemp.al локализуем место-приемник в jnasij по формуле: _masij=masji=m*i+j

mov ax.m

mul di предполагаем, что результат в рамках ах

add ax,si

mov al .temp

mov _mas[bx].al

incdi :j:=j+l

loop rn2

inc si

pop ex восстанавливаем счетчик внешнего цикла

loop ml

Отметим, что для транспонирования прямоугольной матрицы необязательно ее моделировать так, как это сделано в предыдущей программе. Кнут приводит соотношение, которое позволяет транспонировать матрицу в линейном порядке, зная только значения тип. Для этого используется соотношение, при котором значение из ячейки i (для 0<i<N = mn-1) исходной матрицы переводится в ячейку m*x (mod N) транспонированной матрицы.

Упорядоченный поиск

На практике массивы элементов (записей) обычно определенным образом упорядочиваются. Это облегчает задачу поиска в них, так как появляется возможность формализации этого процесса. Записи в массиве в зависимости от значений ключевых полей могут быть упорядочены в числовом или лексикографическом поhядке.

Двоичный поиск

Этот вид поиска (программа prg10_242.asm) предназначен для выполнения поиска в упорядоченном массиве (записей), содержащем N числовых ключей: kl < k2 < <-. <kN. Упорядоченный массив чисел 02h, 04h, 06h, 08h, 16h, 24h, 38h, 45h, 47h, 48h, 56h, 57h, 58h, 70h, 76h, 79h можно представить в виде двоичного дерева (Рисунок 2.5).

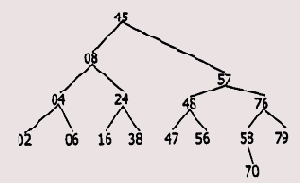
Рисунок 2.5. Представление массива в виде двоичного дерева

Для этого необходимо написать программу, которая в цикле выполняет следующие действия. Вначале определяется элемент, расположенный в середине исходного массива, — он будет вершиной двоичного дерева. Далее в стеке запоминаются интервалы ключей подмассивов, расположенных слева и справа от элемента-вершины двоичного дерева. После этого в цикле происходит извлечение интервалов ключей подмассивов из стека, определение серединных элементов в этих подмассивах, разбиение на очередные подмассивы, запоминание их границ в стеке, извлечение и т. д. В результате этих действий будет построено двоичное дерево, подобное изображенному на рисунке.

Абстрактно задачу поиска ключа с определенным значением К можно сравнить с обходом двоичного дерева начиная с его вершины. Если К меньше значения ключа вершины, то идем к узлу дерева по левой ветке, если больше — то по правой. Значение ключа в очередном узле соответствует среднему элементу под-массива, лежащему слева (справа) от элемента, соответствующего вершине дерева. Для среднего элемента подмассива процедура сравнения и принятия решения о переходе повторяется. Процесс заканчивается, когда обнаружен узел, ключ которого равен К, либо очередной узел является листом и идти больше некуда.

:prg10_242.asm - программа на ассемблере двоичного поиска

;Вход: mas[n] - упорядоченная последовательность двоичных значений длиной N

: к - искомое значение

:Выход: 1 - позиция в mas[n] (0<i<n-l), соответствующая найденному символу.

.data

; задаем массив

masdb 02h.04h.06h.08h.16h.24h.38h.45h.47h.48h.57h.56h.58h.70h.76h.79h

n-$-mas

k db 4 ;искомое значение

.code

в si и di индексы первого и последнего элементов последней просматриевой части

последовательности:

movsi.O .

mov di,n-l

хог ах. ах

nraval.k ;искомое значение в ах cont_search: ;получим центральный индекс:

cmpsi.di ;проверка на окончание (неуспешное):si>di

ja exit_bad

mov bx.si

addbx.di

shr bx.l ;делим на 2

cmpmas[bx].al сравниваем с искомым значением

je exit_good -.искомое значение найдено

ja @@ml ;mas[bx]>k

movsi.bx :mas[bx]<k:

inc si

jmpcont_search @@ml: movdi.bx

decdi

jmp cont_search exit_bad: пор :вывод сообщения об ошибке

exit_good: пор ;вывод сообщения об успехе

Двоичный поиск очень эффективен для поиска в предварительно отсортированном массиве. Другая возможность представления двоичного дерева — список. В списке каждый узел, кроме уникального ключа, содержит информационную часть и ссылки на последующий и, возможно, предыдущий элементы списка. Достоинство представления двоичного дерева в таком виде в том, что списком достаточно легко описывать дерево, в которое включаются и выключаются узлы. При представлении двоичного дерева в виде массива это сделать труднее. Ниже мы рассмотрим представление деревьев в программах на языке ассемблера.

Вложенные структуры

В общем случае поле структуры может само являться структурой. Тогда структура представляет собой иерархическую конструкцию, которую можно изобразить в виде дерева (Рисунок 2.6).

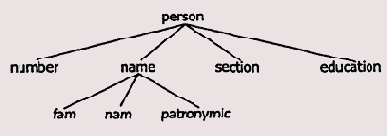
Рисунок 2.6. Иерархическая структура сложной записи

Листы в этом дереве являются той полезной информацией, к которой необходимо получить доступ. Для этого нужно некоторым образом указать последовательность идентификаторов, в которой первым идентификатором является имя структуры, далее следуют идентификаторы промежуточных узлов и последним идентификатором является идентификатор нужного листа. Но в ассемблере подобная схема реализована очень ограниченно — можно указать только имена первого и последнего идентификаторов (промежуточных попросту нет). Рассмотрим пример. Как обычно, прежде чем работать со структурой, необходимо задать ее шаблон. Далее для работы со структурой в программе необходимо создать ее экземпляр. В программе ниже шаблон структуры называется element, а соответствующий ему экземпляр структуры — si. Отметим лишь, что не стоит искать в приведенных ниже примерах какой-либо смысл, так как они предназначены только для демонстрации механизма вложенности структур (и объединений).

:prg02_01.asm - программа, демонстрирующая описание и использование структуры в программе на ассемблере.

elementstruc

INN dd 0 ;ИНН

name db 30 dup С ') ;Ф.И.О.

у_birthday dw 1962 :год рождения

m birthday db 05 ;месяц рождения

d_birthday db 30 :месяц рождения

nationality db 20 национальность

;и так далее

ends

.data

si element<>

.code

mov al,si.m_birthday

Информацию о дате рождения можно оформить в виде отдельной структуры, вложенной в текущую структуру, так как это сделано в программе ниже:

:prg02_02.asm - программа, демонстрирующая вложение структуры в текущую структуру в программе на ассемблере.

elementstruc

INN dd 0 :ИНН

fiodb 30 dup (' ') ;Ф.И.О.

struc

y_birthday dw 1962 ;год рождения m_birthday db 05 ;месяц рождения d_birthday db 30 ;месяц рождения

ends

nationality db 20 национальность ;и так далее

ends

.data

si element<>

.code

mov al ,sl.m_birthday

Синтаксис ассемблера допускает вынести описание вложенной структуры за пределы текущей структуры. При этом можно инициализировать необходимые поля структуры birthday внутри отдельного экземпляра структуры element. Но работает такое описание структуры только в режиме IDEAL, что и продемонстрировано в программе ниже.

:prg02_03.asm - программа, демонстрирующая вложение структуры в другую структуру в программе на ассемблере.

birthday struc

y_bi rthday dw 1962 :год рождения

m_birthday db 05 :месяц рождения

d_birthday db 30 :день рождения

ends

element struc

INN dd 0 ;ИНН

Birthday struc (m_birthday-06. d_birthday=21)

fio db 30 dup С ') ;Ф.И.О.

nationality db 20 национальность

;и так далее

ends

.data

si element <.<»

.code

ideal

mov al,si.m_birthday masm

Кстати, в описание структур можно вкладывать не только описания других структур, но и описание объединений, так как это показано в следующей программе.

:prg02_04.asm - программа, демонстрирующая взаимное вложение объединений и структур в программе на ассемблере.

elementstruc INN del 0 :ИНН fiodb 30 dup С ') :Ф.И.О. union

struc

y_birthday_l dw 1962 :год рождения m_birthday_l db 06 ;месяц рождения d_birthday_l db 03 ;месяц рождения ' ends

struc

d_birthday_2 db ? ;месяц рождения m_birthday_2 db ? :месяц рождения y_birthday_2 dw ? ;год рождения

ends

ends ;конец объединения nationality db 20 -.национальность :и так далее ends .data si element<>

!code"

mov al.si.m_bi rthday_l

mov sl.m_birthday_2,0ffh mov al,sl.m_birthday_2

Выделение классов лексем

Эффективность этапа лексического анализа не в последнюю очередь определяется правильностью разбиения лексем входной программы на классы. Причем эти классы не должны пересекаться. В ходе сканирования каждый входной терминальный символ (лексема) должен быть отнесен к одному из классов. Как мы уже отмечали выше, для грамматики псевдоязыка можно определить следующие классы лексем:

идентификаторы — ID;

ключевые слова - ПРОГРАММА, ПЕРЕМЕННЫЕ, НАЧ_ПРОГ, КОНПРОГ, НАЧ_БЛОК, КОН БЛОК, REAL, INTJYTE, INT_WORD, INT_DWORD, DIV, MOD, ЧИТАТЬ, ПИСАТЬ, ДЛЯ, ДОДЕЛАТЬ, ПОКА, ДОВНИЗ, ЕСЛИ, ЕСЛИ, ДО, ТО, ПЕРЕЙТИ_НА, ПОВТОРИТЬ;

целые числа — CH_INT;

«Навешивание» семантики на дуги «склеенного» конечного автомата

В ходе распознавания (перехода по дугам) требуется выполнять различные действия, например поиск соответствия введенной лексемы ключевому слову в таблице ключевых слов, поиск идентификатора в таблице идентификаторов, преобразования чисел и т. д. Поэтому на этом шаге необходимо определить набор переменных и состав процедур, работающих во время переходов из состояния в состояние (на дугах).

Все... После этого можно программировать сканер. В главе 10, посвященной командам ММХ- и ХММ-расширений, нами будет выполнена практическая работа в этом направлении.