CRC-арифметика
CRC-арифметика
Расчеты CRC ведутся в двоичной системе счисления. При проведении CRC-вы-числений используется специальная CRC-арифметика, которая, по сути, является полиномиальной арифметикой по модулю 2. Полиномиальная арифметика по модулю 2 — это еще один из видов арифметик, используемых для решения задач в определенной предметной области и отличающихся от привычной двоичной арифметики с циклическим переносом отсутствием переносов и вычислением всех коэффициентов по модулю 2 . В уроке 20 «ММХ-технология микропроцессоров Intel» учебника при рассмотрении ММХ-команд мы знакомились с одной из таких альтернативных арифметик — арифметикой с насыщением. Теперь рассмотрим особенности CRC-арифметики.
Итак, как отмечено выше, в основе CRC-арифметики лежит полиномиальная арифметика. По определению, полином — линейная комбинация (сумма) произведений целых степеней заданного набора переменных с постоянными коэффициентами. Частный случай — полином, содержащий одну переменную:
u(x)=unxn+...u,x1+uoxo.
Здесь un, nu щ — элементы некоторой алгебраической системы S, называемые коэффициентами; х — переменная полинома, которую можно рассматривать как формальный символ без определенного значения. Алгебраическая система S обычно представляет собой множество целых или рациональных чисел в диапазоне 0..m-1 со сложением, вычитанием и умножением, выполняемыми по модулю т. Для нашего рассмотрения особенно важна полиномиальная арифметика по модулю 2, в которой каждый коэффициент полинома равен одному из двух значений — 0 или 1. Например, шестнадцатеричное значение ОеЗп может быть представлено следующим полиномом:
1х27 + 1х26 + 1х25 + 0х24 + 0х23 + 0х22 + 1x21 + 1x2°.
Если ввести в качестве переменной х=2, то получим следующий двоичный полином:
1хx7 + 1xx6 + 1xx5 + 0хх4 + 0xx3 + 0xx2 + 1xx1 + 1хх°.
В этом полиноме, строго говоря, значение х не играет особой роли, так как данное двоичное число можно представить полиномом в другой системе счисления, например, шестнадцатеричной: ехх1 + 2хх°, где х = 16. При этом заметим, что в том и другом случае цифры 0, 1, е, 2 — это просто цифры двоичной и шестнадцатеричной систем счисления.
Так как слагаемые двоичного полинома с нулевыми коэффициентами не дают никакого вклада в конечный результат, то их можно попросту отбросить, оставив только слагаемые, переменные которых имеют единичные коэффициенты:
1xx7 + 1xx6 + 1xx5 + 0xx4 + 0xx3 + 0xx2 + 1xx1 + 1хх° -
= 1xx7 +1xx6 + lxx5 + 1xx1+ 1xx0 = = x7 + x6 + x5 + x1 + x°.
Здесь x = 2. Над полиномами можно выполнять арифметические операции: сложение, умножение и вычитание. Процессы выполнения этих операций для полиномиальной арифметики и обычной арифметики многократной точности (см. главу 1) похожи. Главное отличие в том, что из-за отсутствия связи между коэффициентами полинома понятие переноса в полиномиальной арифметике отсутствует.
Например, для умножения 7h (0111b) на 5h (0101b) выполняются действия:
(х2 + х1 + х°)х(х2 + х°) = (х4 + х3 + х2 + х2 + х1 + х°) -=х4 + х3 + х2 + х2 + х1 + х° + х°= х4 + х3 + 2х2 + х1 + 2х°.
Для того чтобы получить в ответе 35, мы должны х взять равным 2 и привести коэффициенты у членов полинома 2х° и 2х2 к двоичным, сделав перенос соответствующих единиц в старшие разряды: 01010 переносы 11111 результат
100011 = 35)0.
В результате получим двоичный полином х5+х'+х°.
Эти рассуждения призваны сформулировать очередной тезис о том, что переносы, как и в обычной арифметике, можно выполнять в случае, когда известно основание системы счисления. То есть до тех пор, пока мы не знаем х, мы не можем производить и переносы. В приведенном выше примере, мы не знаем, что 2х2 и 2х° на самом деле являются х3 и х1 до тех пор, пока не известно, что х = 2. То есть в полиномиальной арифметике коэффициенты при разных степенях изолированы друг от друга и отношения между ними не определены. Из-за этого возникает первая странность полиномиальной арифметики — операции сложения и вычитания в ней абсолютно идентичны и вместо них можно смело оставлять одну. Например, сложение по правилам полиномиальной арифметики по модулю 2, будем ее далее называть CRC-арифметикой, будет выполнено так:
| 11111011 | |
| + | 11001010 |
| 00110001 |
Из этого примера видны правила сложения двоичных разрядов в арифметике t с отсутствием переносов:
0+0=0; 0+1 = 1; 1+0=1; 1 + 1=0.
Операцию вычитания демонстрирует следующий пример:
| 11111011 | |
| - | 11001010 |
| 00110001 |
0-0=0; 0-1=1; 1-0=1; 1-1=0.
Сравнение примеров для сложения и вычитания полиномов по модулю 2, а также правил, по которым они выполняются, показывает то, что эти две операции CRC-арифметики идентичны и по принципу формирования результата они аналогичны команде ассемблера XOR. Цель, которой достигают всеми этими условностями, — исключить из поля внимания все величины (путем заемов/перено-сов), лежащие за границей старшего разряда.
Умножение в арифметике с отсутствием переносов также выполняется с учетом особенностей CRC-сложения:
| 1101 | |||
| x | 1011 ----- |
||
| 1101 | |||
| 1101 | |||
| 0000 | |||
| 1101 | |||
| 1111111 |
Для нашего рассмотрения особый интерес представляет операция деления, так как в основе любого алгоритма вычисления CRC лежит представление исходного сообщения в виде огромного двоичного числа, делении его на другое двоичное число и использовании остатка от этого деления в качестве значения CRC. Деление — самая сложная из операций CRC-арифметики. Здесь необходимо ввести так называемое слабое понятие размерности: число X больше или равно числу Y, если оба числа имеют одинаковую размерность и позиции их старших битов единичны, то есть соотношение остальных битов X и Y для операции сравнения не имеет значения. Рассмотрим примеры операции деления, причем для лучшего понимания сделаем это в двух вариантах: вначале вспомним, как выполняется обычное деление (по правилам двоичной арифметики с циклическим переносом), а затем выполним собственно CRC-деление.
Возьмем произвольную двоичную последовательность и разделим ее на некоторое число по правилам двоичной арифметики с циклическим переносом
(Рисунок 9.3).
По правилам CRC-арифметики деление для приведенных выше исходных данных даст следующий результат (Рисунок 9.4).
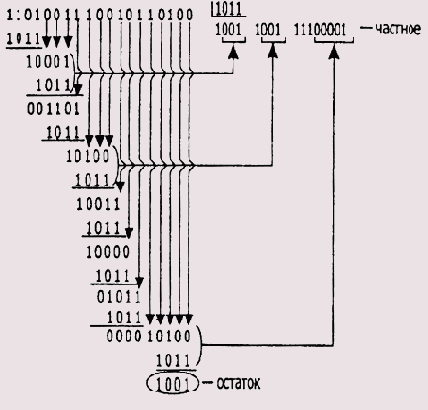
Рисунок 9.3. Схема вычисления двоичного деления (с циклическим переносом)
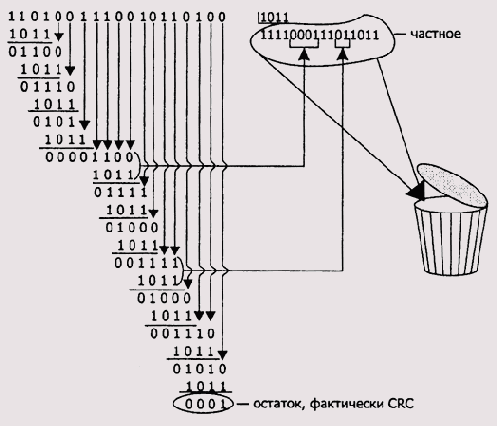
Рисунок 9.4. Схема вычисления CRC-деления
Как видите, результаты обычного и CRC-делений отличаются. Главное, чтобы вы подметили особенность выполнения CRC-деления. Особое внимание обратите на порядок формирования промежуточных результатов в процессе деления. Снос двоичных разрядов из делимого продолжается до тех пор, пока размерности промежуточного битового значения и делителя не сравняются, а их старшие разряды не станут равными 1. После этого над двоичными разрядами выполняется побитовое CRC-вычитание. Соотношение разрядов не важно, главное — это одинаковая размерность и единичные старшие биты. В этом случае считается, что вычитаемое больше вычитаемого, что влечет за собой включение 1 в частное и выполнение операции CRC-вычитания. Это как раз и есть проявление слабого
понятия размерности. Корзина для мусора, показанная на Рисунок 9.4, означает тот факт, что частное для процесса вычисления CRC-битовой последовательности не имеет никакого значения.
Реальные двоичные последовательности являются результатом сцепления порой огромного количества отдельных байтов (символов), образуя одно большое двоичное число, для представления которого нужно использовать двоичные полиномы огромных степеней. При этом каждый бит в подобной последовательности произвольной длины представляется в виде коэффициента длинного полинома. Например, для представления 128-разрядного блока необходим полином, состоящий из 1024 слагаемых, а для 1024-битного блока необходим полином уже с 8192 слагаемыми. В терминах полиномиальной арифметики двоичное число, сформированное в результате подобной сцепки составляющих блока данных, называется полиномом данных {сообщения) и обозначается как D(x) [5, 44]. В алгоритме вычисления CRC вводится еще несколько полиномов и соотношений между ними:
порождающий полипом G(x) — предварительно особым образом выбранный полином, на который делится исходный полином сообщения;
полином-частное Q(x) — полином, получившийся в качестве частного от деления полиномов D(x)/G(x);
полином-остаток R(x) — полином, получившийся в качестве остатка от деления полиномов D(x)/G(x).
Между перечисленными полиномами существуют следующие отношения:
D(x)=Q(x)xG(x)+R(x), Q(x)=(D(x)-R(x))/G(x).
Эти соотношения приводят к следующим основополагающим для дальнейшего рассмотрения тезисам:
операция деления двух двоичных полиномов D(x)/G(x), где G(x)*0, дает в качестве результата полином-частное Q(x) и полином-остаток R(x), удовлетворяющие условиям: D(x)=Q(x)xG(x)+R(x);
остаток от деления двух полиномов R(x) является двоичным числом, которое после вычитания из D(x) дает в результате еще один полином, делящийся без остатка на G(x); получающееся в результате этого деления частное Q(x) отбрасывается за ненадобностью, а полином-остаток R(x) на-- зывают CRC (Cyclic Redundancy Code).
Из приведенного выше описания общей схемы вычисления CRC возникает ряд вопросов: что представляет собой этот магический делитель G(x), каков его размер? Выбор порождающего полинома G(x) — достаточно сложная задача. Перечислим некоторые важные свойства, которые должны учитываться при этом.
Число разрядов (количество членов) в полиноме-остатке R(x) непосредственно определяется длиной самого порождающего полинома G(x). Выбор G(x) длиной п гарантирует, что полином-остаток от деления R(x) будет иметь разрядность не более, чем п-1. Это следует из общего свойства операции деления, которое предполагает, что остаток от деления должен быть меньше делителя.
Порождающий полином G(x) должен быть полиномиально простым. Это означает его неделимость нацело на полиномы со значением в диапазоне от 2 до самого себя.
Способность порождающего полинома G(x) к выявлению ошибок, специфичных для передачи данных по каналами связи. Это такие ошибки, как ошибки в одном, двух, нечетном количестве битов, а также ошибки блока битов. Выше мы отмечали, что более простые методы обнаружения ошибок передачи не способны обнаружить с достаточной степенью вероятности большинство таких типов ошибок.
Для большинства алгоритмов вычисления CRC значение порождающего полинома известно заранее и, более того, утверждено соответствующими стандартами. Поэтому программисту без особой надобности не стоит терять времени и сил на изобретение нового значения порождающего полинома G(x). Приведем значения некоторых широко известных полиномов, используемых на практике.
х'6+х12+х5+х° — полином 1021h, используемый в протоколе XMODEM и производных от него протоколах передачи данных. Он стандартизован в спецификации V.41 МККТТ «Кодонезависимая система контроля ошибок».
Ш х16+х|5+х2+х° — полином 8005h, используемый в протоколе двоичной синхронной передачи фирмы IBM. Он также стандартизован в приложении А «Процедура коррекции ошибок для оконечного оборудования линии с использованием асинхронно-синхронного преобразования» к стандарту V.42 МККТТ. Этот же полином широко известен как полином, используемый в алгоритме вычисления CRC — CRC16.
x32+x26+x23+x22+x16+x12+x"+xlo+xs+x7+x5+x4+x2+x1+x0 - полином 04clldb7h, используемый в алгоритме вычисления CRC — CRC32 и также стандартизованный в стандарте V.42 МККТТ. Этот полином, в частности, используется в технологии локальных вычислительных сетей Ethernet. Необходимо отметить, что вычисление по алгоритму CRC32 зачастую проводят и с другим полиномом: 0edb88320h:
x32+x31+x30+x29+x27+x26+x24+x23+x21+x20+ +х19+х15+х9+х8+х5. Последний полином используют различные архиваторы. Необходимо заметить, что полином 0edb88320h — это просто зеркальное отражение полинома 04clldb7h.
В заключение отметим, почему выгодно увеличивать число разрядов CRC. Выше уже было отмечено, что алгоритм вычисления CRC по сути своей является одним из возможных (и неплохих) алгоритмов хэширования. Разрядность порождающего полинома G(x) 16 бит обеспечивает до 65 535 значений хэш-функции. Увеличение разрядности полинома G(x) до 32 битов приводит к расширению набора значений хэш-функции уже до 4 294 967 295.
С полиномом связано еще одно понятие — степени полинома, которое по определению является номером позиции его старшего единичного бита (считая с нуля). Например, для полинома 1011 из приведенного выше примера (см. Рисунок 9.4) степень равна 3.
В качестве выводов отметим, что CRC-арифметика отличается от двоичной отсутствием переносов/заемов, а CRC-вычитание и сложение выполняются по
тем же правилам, что и команда ассемблера XOR, что и обусловливает ее важную роль при вычислении значений CRC.
Вычисление CRC
Глава 9. Вычисление CRC

Основы
Основы
Для того чтобы лучше понять суть табличного алгоритма вычисления CRC, обратимся опять к прямому методу, точнее к той схеме его вычисления (см. Рисунок 9.6), которая была реализована в приведенной выше программе.
Из этой схемы видно, что для текущего содержимого старшей половины регистра ЕАХ можно прогнозировать, как будет изменяться содержимое его битов по мере их сдвига. Для этого достаточно подвергнуть анализу его биты начиная с самого старшего. Допустим, что старшие 8 бит ЕАХ равны а7 а6 а5 а4 а3 а2 а, а,,. При следующем сдвиге (см. Рисунок 9.6) прямой алгоритм определяет, будет ли произведена операция XOR операнда с полиномом b7 b6 b5 b4 Ь3 b2 b, bо в ВХ (а7=1) или нет (а7=0). Если выдвинутый бит был равен 1, то прежнее содержимое старшей половины регистра ЕАХ будет подвергнуто операции XOR с соответствующими битами полинома. В обратном случае, если выдвинутый бит был равен 0, значения битов будут не изменены, а просто сдвинуты влево на одни разряд. В принципе, имея большое желание, можно рассчитать заранее, каким будет содержимое к-го бита в к-й итерации сдвига. К примеру, значение нового старшего бита, определяющего действия алгоритма в следующей итерации, можно рассчитать по содержимому двух старших битов старшего байта исходного операнда — а6 XOR а7 AND b7, где b7 — старший бит полинома (всегда равный единице).
Теперь остановимся для того, чтобы рассмотреть и обсудить очередную схему (Рисунок 9.7).

Рисунок 9.7. Влияние на регистр ЕАХ серии операций XOR при вычислении CRC
Из рассуждений выше следует, что если взять для рассмотрения старший байт операнда, то по его содержимому можно однозначно предположить, сколько операций XOR и когда будет выполнено (см. рисунок). Обозначим старшую половину регистра ЕАХ как переменную А, а операнды со значениями полинома, объединяемые с А при единичном состоянии очередного выдвигаемого слева бита, обозначим соответственно как В, С, D (помним, что В = С = D). Тогда формирование результата Е можно представить формулой:
Е-((А [сдвиги| XOR В) [сдвигиj XOR С) |сдвиги| XOR D
Здесь | сдвиги | представляют собой значение от 0 до 7 и определяются теку щим содержимым старшего байта операнда (регистра ЕАХ). Благодаря ассоциативному свойству операции XOR тот же самый результат можно получить, если предварительно выполнить операцию XOR над полиномами В, С, D с соответствующими значениями сдвигов, а затем результат объединить по XOR с А:
F: = 1 сдвиги| XOR ( В |сдвиги| XOR С |сдвиги| XOR D) Е:= A XOR F
Из этих рассуждений следуют важные выводы:
величина F является совершенно точно предсказуемой по содержимому старшего байта операнда;
если величина F определяется содержимым старшего байта операнда и собственно значением полинома, то существует всего 256 возможных значений этой величины (по количеству значений, представимых беззнаковым байтом);
исходя из первых двух положений величина F не зависит от значения операнда и может быть рассчитана заранее, при этом результаты ее расчетов можно свести в таблицу (!).
Вот мы и выяснили, на чем основано название табличного алгоритма расчета CRC. Теперь со знанием сути дела приведем его общее описание (Рисунок 9.8). В качестве основы для рассуждений по-прежнему используем программу прямого вычисления значения CRC и соответствующую схему (см. Рисунок 9.6).

Рисунок 9.8. Общая схема табличного алгоритма
На схеме, показанной на рисунке, цифрами обозначена последовательность шагов табличного алгоритма. Шаги 1 и 2 выполняются одновременно и означают, что старший байт из регистра ЕАХ выдвигается в переменную R, а младший байт этого регистра заполняется очередным байтом исходной последовательности. Значение переменной R используется на шаге 3 в качестве индекса в таблице TABL_F для извлечения 16-битного значения, которое на шаге 4 будет объединено
операцией XOR с содержимым старших 16 битов регистра ЕАХ. Таким образом, в отличие от прямого алгоритма процесс преобразования вырастает до уровня байтов и содержит три операции: сдвига, доступа к таблице для извлечения нужного значения и операции XOR извлеченного значения с содержимым старшей половины ЕАХ. По окончании процесса в старшей половине ЕАХ будет содержаться значение CRC. Сообщение по-прежнему должно быть выровненным, то есть дополненным количеством битов, равным степени полинома, или для данного случая — 16. Для практических приложений это крайне неудобно, и решение этой проблемы будет показано чуть ниже. Пока же разработаем программу вычисления содержимого таблицы на основе полинома 1021h степени 16.
:prg09_03.asm - программа вычисления содержимого таблицы : на основе полинома 1021п степени 16.
.data
tabl_16 dw 256 dup (0) :CRC-таблица
len_tabl_16=$-tabl_16
adr_tabl_16 dd tabl_16
polinom dw 1021h
.code
les di,adr_tabl_16
add di.len_tabl_16-2
std :идем назад по таблице
mov ex.255
mov bx.polinom
ml: xor ax.ax
mov ah.cl :индекс в таблице для вычисления CRC
push ex сложенные циклы
mov ex. 8
m2: shl ax.l
jnc m3 :старшие разряды не равны - выполняем сдвиг
: (частное нас не интересует) ;старшие разряды равны - выполняем XOR:
xor ax.bx :ax XOR polinom
m3: loop m2 _^
pop ex
stosw
loop ml
В результате работы этой программы область памяти tabl_16 будет инициализирована таблицей значений, которые могут быть использованы в схеме вычис-- ления значения CRC исходной последовательности (см. Рисунок 9.8).
Прямой алгоритм вычисления CRC
Прямой алгоритм вычисления CRC
Даже маленькая практика стоит большой теории.
Закон Букера (Прикладная Мерфология)
После всех этих рассуждений мы готовы к тому, чтобы осмысленно воспринять общую схему реального алгоритма вычисления CRC — алгоритма прямого (поразрядного) вычисления CRC. При этом удобно CRC-алгоритм рассматривать с точки зрения двух сторон-участников процесса: источника — объекта, формирующего сообщение для передачи, и приемника — объекта, который принимает сообщение и проверяет его целостность. Действия источника следующие.
1. Выбрать полином Р, в результате автоматически становится известной его степень N.
2. Добавить к исходной двоичной последовательности N нулевых битов. Это добавление делается для гарантированной обработки всех битов исходной последовательности.
3. Выполнить деление дополненной N нулями исходной строки S на полином Р по правилам CRC-арифметики. Запомнить остаток, который и будет являться CRC.
4. Сформировать окончательное сообщение, которое будет состоять из двух частей: собственно сообщения и добавленного в его конец значения CRC.
К примеру, вычисление по этому алгоритму CRC для исходной последовательности 1101001110010110100 (см. Рисунок 9.4) и сама окончательная последовательность на стороне источника будут выглядеть так, как показано на Рисунок 9.5.
Из рисунка видно, что в начале вычисления исходная последовательность 1101001110010110100 дополняется нулями в количестве, равном степени полинома (Р=1011 - степень полинома N=3): 1101001110010110100+000. При выполнении CRC-деления эти дополнительные биты гарантируют, что все биты исходной последовательности примут участие в процессе формирования значения CRC. Результирующая последовательность получается равной исходной последовательности, дополненной значением CRC: 1101001110010110100+011. Заметим, что длина присоединяемого к исходной последовательности значения CRC должна быть равна степени полинома, даже если CRC, как в нашем случае, имеет ведущие нули. Это очень важный момент, понимание которого является ключом к пониманию сути процессов, происходящих на стороне приемника при получении и определении целостности исходного сообщения. Действия алгоритма для приемника просты — выполнить деление полученной последовательности на полином. При этом для выполнения деления нет необходимости дополнять исходную последовательность нулями, тем более что на практике соблюдение этого условия крайне неудобно. Приемник попросту выполняет CRC-деление полученной исходной строки (дополненной в конце
исходным значением CRC) на полином и анализирует остаток. Если остаток от этого деления нулевой, то исходная последовательность не была нарушена во время передачи. В обратном случае существует очень большая вероятность нарушения целостности исходной последовательности, и нужно принимать дополнительные меры по выяснению и исправлению ситуации. Одной из таких мер может быть попытка восстановления нужного значения CRC.
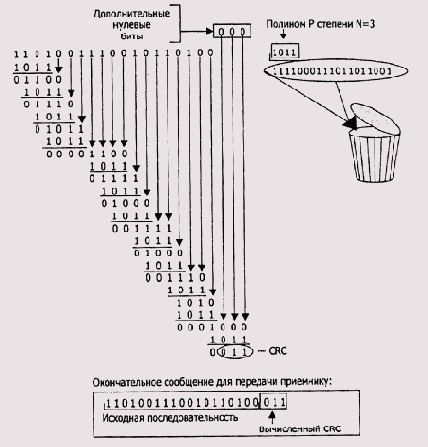
Рисунок 9.5. Схема формирования выходного сообщения из исходного с использованием CRC-алгоритма
Описанный выше алгоритм вычисления значения CRC называется прямым и чаще всего реализуется аппаратно. Но, тем не менее, для совершенствования навыков программирования на ассемблере составим реализующий его пример программы. Хотя эффективность этой программы не слишком высока, у нее есть две учебные цели:
показать в виде программной реализации суть алгоритма вычисления CRC и самого CRC-деления;
подготовить себя к пониманию более совершенных алгоритмов расчета CRC, к которым относится, в частности, рассматриваемый ниже табличный алгоритм.
Для компьютерной реализации алгоритмов вычисления CRC удобно выбирать полиномы со степенями, кратными 8 (то есть размерности регистров) — 8, j5, 24, 32 или даже 64. В этом случае можно подобрать команды из системы команд микропроцессора, наиболее оптимально реализующие алгоритмы вычисления CRC. В качестве полинома выберем один из рекомендуемых полиномов (см. ниже) — 4003. И еще одно важное замечание — степень полинома определяет размерность регистра, используемого в алгоритме, при этом считается, что старший (всегда единичный) бит полинома находится сразу за левой границей регистра. В этих условиях программа реализации прямого алгоритма вычисления CRC функционирует следующим образом (для лучшего понимания в процессе разбора алгоритма см. Рисунок 9.6). В регистр побитно вдвигаются биты исходной строки. Это происходит до тех пор, пока при очередном сдвиге слева появится единичный бит. В этом случае все содержимое регистра подвергается операции XOR со значением полинома без старшего бита. Далее процесс сдвига и анализа выдвигаемого бита продолжается до тех пор, пока не будет выдвинут очередной единичный бит, в результате чего опять между регистром и полиномом выполняется операция XOR, и т. д. После того как последний бит вдвинут в регистр, в него вдвигается количество нулевых битов, равное степени полинома. Этим, как мы не раз уже отмечали, достигается участие всех бит исходной битовой строки в формировании значения CRC. В результате в регистре остается значение CRC, которое необходимо добавить к исходной строке и передать приемнику.
jnc m5 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)
;старшие разряды равны - выполняем XOR:
хог eax.ebx;eax(31. .16) XOR pollnom т5: loop m4
В результате вычисления CRC символьной последовательности "6476с8" получим CRC • 35dah.

Рисунок 9.6. Схема вычисления значения CRC прямым алгоритмом
Для того чтобы смоделировать действия стороны приемника, можно использовать ту же самую программу со слегка измененными исходными данными — к строке bitstring добавляем вычисленное значение CRC. После этого под отладчиком наблюдаем за процессом CRC-деления, причем контролируем остаток от деления. В определенный момент увидим, что он стал нулевым — это свидетельствует о том, что исходная последовательность не была изменена. Для эксперимента можно изменить значения одного или более битов исходной последовательности и посмотреть, что получится.
;prg09_02.asm - программа демонстрации прямого алгоритма вычисления CRC ;(сторона-приемник).
.data
исходная битовая последовательность в символах
bit_string db "6476c8",35h.0dah
1en_bit_stri ng=$-bi t_stri ng
adr_bit_string dd bit_string
polinomdw 4003h
.code
main:
:см. предыдущую программу
exit: :выход из программы
Очевидный недостаток прямого метода — большое количество операций сдвига, исключающих операций ИЛИ (XOR) и операций условного перехода, которые выполняются для каждого бита исходного сообщения. Поэтому на практике используется другой способ расчета CRC, называемый табличным.
std :идем назад по таблице
mov ex.255
mov bx.polinom
ml: xor ax,ax
mov ah.cl :индекс в таблице для вычисления CRC
push ex сложенные циклы
mov ex.8
m2: shi ax.l
jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)
:старшие разряды равны - выполняем XOR:
xor ax.bx :ax XOR polinom
тЗ: loop m2
pop ex
stosw
loop ml
-------------закончили расчет CRC-таблицы.........
хог ах,ах
xor bx.bx
Ids si.adrbitstring
mov cx.len_bit_string
m4: mov bl.ah
shl ax.8
xor bl.[si]
xor ax.tabl_16[bx]
inc si
1oop m4
;.........
Рассмотрением этого алгоритма введение в проблему вычисления CRC можно было бы и закончить. Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:
переход от цикла по всем битам к циклу по большим порциям данных — байтам, словам и т. д.;
повышение разрядности порождающего полинома;
отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).
Алгоритмы вычисления CRC получили свое закрепление в некоторых стандартах. Перечислим отличительные особенности основных алгоритмов вычисле-^ ния CRC. Итак, основные алгоритмы вычисления CRC различаются:
по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;
по начальному содержимому регистра, в котором формируется значение CRC;
по тому, производится ли обращение битов каждого байта перед его обработкой;
по способу прохода байтов через регистр — способ может быть косвенным или прямым;
по тому, производится ли обращение конечного результата;
по конечному значению, с которым производится объединение по XOR результата вычисления CRC.
После появления 32-разрядных микропроцессоров наибольшей популярностью стали пользоваться 32-разрядные алгоритмы вычисления CRC. В различных источниках рассматривают два типа таких алгоритмов — прямой и зеркальный. Рассмотрим их конкретные реализации, рекомендуемые стандартами.
Необходимость дополнения исходной строки завершающими
Прямой табличный алгоритм CRC16
' Необходимость дополнения исходной строки завершающими нулевыми байтами представляет большое неудобство при реализации общей схемы табличного
алгоритма. Поэтому на практике используют другую схему вычисления CRC, не требующую завершения исходного сообщения нулевыми байтами. В этой схеме
очередной байт исходной строки объединяется операцией XOR со старшим байтом регистра, выдвинутым с левой стороны этого регистра. Полученное в результате объединения значение используется в качестве индекса для доступа к CRC-таб-лице. Извлекаемое из CRC-таблицы значение объединяется операцией XOR с содержимым регистра. Описанный алгоритм называют прямым табличным алгоритмом.

Рисунок 9.9. Схема вычислений CRC с использованием прямого табличного алгоритма
На схеме вычислений CRC с использованием прямого табличного алгоритма цифрами обозначена последовательность шагов вычисления CRC.
1. Выдвижение старшего байта регистра АХ в байтовую ячейку.
2. Выполнение операции XOR над выдвинутым на шаге 1 в байтовую ячейку старшим байтом регистра АХ и очередным байтом исходной строки.
3. Полученное на шаге 2 значение используется в качестве индекса для доступа к элементу CRC-таблицы.
4. Извлеченное из CRC-таблицы значение объединяется по XOR со значением в регистре АХ.
5. Результат выполнения на шаге 4 операции XOR помещается обратно в регистр АХ.
После обработки последнего байта исходной строки регистр АХ содержит значение CRC. Программа вычисления CRC с использованием прямого табличного алгоритма приведена ниже.
:prg09_04.asm - программа вычисления CRC с использованием прямого табличного алгоритма.
.......... »
.data
;исходная битовая последовательность в символах
bit_string db "6476c8"
1en_bi t_string=$-bi t_stri ng
adr_bit_string dd bit_string
tabl_16 dw 256 dup (0) iCRC-таблица
Ien_tab1_16=$-tabl_16 adr_tabl_16 dd tabl_16
polinom dw 1021h
.code
.-------------расчитываем CRC-таблицу---.....-------------
les di.adr_tabl_16
add di.len_tabl_16-2
std :идем назад по таблице
mov ex.255
mov bx.polinom
ml: xor ax,ax
mov ah.cl :индекс в таблице для вычисления CRC
push ex сложенные циклы
mov ex.8
m2: shi ax.l
jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)
:старшие разряды равны - выполняем XOR:
xor ax.bx :ax XOR polinom
тЗ: loop m2
pop ex
stosw
loop ml
-------------закончили расчет CRC-таблицы.........
хог ах,ах
xor bx.bx
Ids si.adrbitstring
mov cx.len_bit_string
m4: mov bl.ah
shl ax.8
xor bl.[si]
xor ax.tabl_16[bx]
inc si
1oop m4
;.........
Рассмотрением этого алгоритма введение в проблему вычисления CRC можно было бы и закончить. Все существующие алгоритмы вычисления CRC являются, по сути, различными модификациями описанного выше табличного алгоритма. Эти модификации преследуют разные цели, перечислим некоторые из них:
переход от цикла по всем битам к циклу по большим порциям данных — байтам, словам и т. д.;
повышение разрядности порождающего полинома;
отражение особенностей функционирования аппаратуры передачи данных (наличие этой цели обусловлено тем, что микросхемы, поддерживающие работу последовательного порта компьютера, передачу байта начинают с его младших битов, поэтому описанные ниже алгоритмы расчета CRC, учитывающие эту особенность, называются зеркальными).
Алгоритмы вычисления CRC получили свое закрепление в некоторых стандартах. Перечислим отличительные особенности основных алгоритмов вычисле-^ ния CRC. Итак, основные алгоритмы вычисления CRC различаются:
по значению и степени порождающего полинома, при этом значение полинома обычно указывается без ведущей единицы в старшем разряде;
по начальному содержимому регистра, в котором формируется значение CRC;
по тому, производится ли обращение битов каждого байта перед его обработкой;
по способу прохода байтов через регистр — способ может быть косвенным или прямым;
по тому, производится ли обращение конечного результата;
по конечному значению, с которым производится объединение по XOR результата вычисления CRC.
После появления 32-разрядных микропроцессоров наибольшей популярностью стали пользоваться 32-разрядные алгоритмы вычисления CRC. В различных источниках рассматривают два типа таких алгоритмов — прямой и зеркальный. Рассмотрим их конкретные реализации, рекомендуемые стандартами.
и любой табличный алгоритм, табличный
Прямой табличный алгоритм CRC32
Как и любой табличный алгоритм, табличный алгоритм вычисления CRC32 требует задания CRC-таблицы. Ее можно задать в програм'ме статически, явно прописав значения элементов таблицы в сегменте кода, или динамически, вычислив значения элементов таблицы перед началом расчета CRC. Ниже приведена программа вычисления CRC-таблицы для полинома 04clldb7.
Прямой табличный алгоритм CRC32 удобно рассматривать со стороны участников процесса, как это мы делали выше. Источник выполняет следующие действия.
:prgO9_O5.asm - программа вычисления CRC-таблицы для полинома 04clldb7.
.data
;С1<С32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
les di.adr_tabl_32_direct
add di,len_tabl_32_direct-4
std :идем назад по таблице
mov ex,255
mov ebx.polinom /
ml: xor eax.eax
shrd eax.ecx,8
push ex сложенные циклы
mov ex.8 m2: shl eax.l
jnc m3 :старшие разряды неравны - выполняем сдвиг (частное нас не интересует)
;старшйе разряды равны - выполняем XOR:
xor eax.ebx :ax XOR polinom
шЗ:loop m2
pop ex
1. Делает начальную установку регистра, в котором будет производиться формирование CRC, значением OFFFFFFFFh.
2. Вычисляет значение CRC для каждого байта исходной последовательности, принцип которой показан на схеме (см. Рисунок 9.9). Читатель понимает, что хотя эта схема иллюстрирует принцип вычисления CRC16, но для 32-разрядного алгоритма нужно только увеличить размер элементов таблицы до 32 бит и задействовать весь регистр ЕАХ.
3. Объединяет по XOR итоговое значение в ЕАХ со значением OFFFFFFFFh.
4. Добавляет вычисленное значение в конец двоичной исходной последовательности. После этого его можно передать по назначению.
Ниже приведена программа вычисления CRC32 по прямому табличному алгоритму.
;prg09_06.asm - программа вычисления CRC32 по прямому табличному алгоритму.
исходная битовая последовательность в символах
bit_string db "123456789"
len_bit_string=$-bit_string
сгс_32 dd 0 ; сюда мы поместим рассчитанное значение CRC32
adr_bit_string dd bit_string
;СЯС32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
:----.........расчитываем CRC32 таблицу
les di.adr_tabl_32_direct
add di.len_tabl_32_direct-4 * std ;идем назад по таблице
mov ex.255
mov ebx, polinom
ml: xor eax.eax
shrd eax.ecx.8
push ex сложенные циклы
mov ex.8
m2: shl eax.l
jnc m3 :старшие разряды неравны - выполняем сдвиг (частное нас не интересует)
:старшие разряды равны - выполняем XOR:
xor eax.ebx :ax XOR polinom
m3: loop m2
pop ex
stosd
loop ml
:.....--......закончили расчет CRC32 таблицы
mov eax, OFFFFFFFFh
Ids si.adr_bit_string
mov cx.len_bit_string
m4: xor ebx.ebx
shld ebx.eax.8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
1 oop m4 :запишем crc-32 в конец (или начало, см. обсуждение ниже) последовательности:
xor eax. OFFFFFFFFh
mov crc_32.eax ;добавляем в конец исходной последовательности
Значение CRC32 для строки "123456789" равно 9c970409h.
Если для источника стандарт определяет практически однозначную последовательность действий, то для приемника возможны несколько вариантов поведения. Отметим два из них.
В первом варианте критерием для вывода о целостности полученного приемником сообщения является результат сравнения или нулевой результат.
1. Выполнить начальную установку регистра, в котором будет производиться формирование значения CRC.
2. Вычислить значение CRC для каждого байта полученной последовательности, принцип которой показан на схеме (см. Рисунок 9.9 и замечания выше о различиях CRC16 и CRC32).
3. Объединить по XOR итоговое значение в ЕАХ со значением OFFFFFFFFh.
4. Далее можно сделать одно из двух действий:
сравнить значение в ЕАХ со значением CRC, полученным вместе с сообщением, — если они равны, то полученное сообщение идентично исходному;
пропустить байты со значением CRC через процесс получения CRC наравне с другими байтами — об успехе будет свидетельствовать нулевое значение (этот вариант предпочтительнее, так как не предполагает получение предварительных сведений о длине начальной последовательности без учета исходного значения CRC).
Во втором варианте критерием для вывода о целостности полученного приемником сообщения является фиксированная двоичная константа 6b202ca2h.
1. Выполнить начальную установку регистра, в котором будет производиться формирование CRC, в значение OFFFFFFFFh;
2. Вычислить значение CRC32 для каждого байта полученной последовательности (вместе со значением CRC32 в конце), принцип которой показан на схеме (см. Рисунок 9.9 и замечания выше о различиях CRC16 и CRC32). Должно получиться фиксированное двоичное значение — 6b202ca2h. Необ ходимо заметить, что в литературе можно встретить другое значение — 0debb20e3h, но у автора получалось первое.
Основное отличие этих двух вариантов в том, что нужно каким-то образом отделять контролируемую строку и ее значение CRC32. Избежать прямого отслеживания длины принимаемой строки на стороне приемника можно путем формирования источником значения CRC32 в начале исходной строки либо вообще вне строки. Последний случай, например, характерен для программы, которая отслеживает целостность файлов в некотором каталоге. Тогда результаты подсчета CRC для каждого файла хранятся в некотором служебном файле. Если такой вариант вас не устраивает, тогда следует написать код приемника для прямого табличного алгоритма так, как это сделано для приемника в зеркальном табличном алгоритме. Попробуйте самостоятельно определить константу, соответствующую успешному принятию приемником исходной строки.
Учитывая практическую важность обоих вариантов и для демонстрации разнообразия подходов к проблеме вычисления CRC32, работу приемника для прямого табличного алгоритма продемонстрируем на примере первого варианта, приемник «зеркального» табличного алгоритма CRC32 разработаем исходя из положений второго варианта. Но вы должны понимать, что правильное понимание принципов расчета CRC позволяет вам при соответствующей доработке кода поменять варианты работы приемников. В поле сгс_32 должно быть значение CRC32, рассчитанное предыдущей программой. Автор специально не стал объединять эти программы. Пусть это сделает читатель в нужном для его текущей работы контексте.
;prg09_06.asm - программа вычисления CRC32 по прямому табличному алгоритму.
исходная битовая последовательность в символах
bit_string db "123456789"
len_bit_string=$-bit_string
сгс_32 dd 0 ;сюда мы поместим рассчитанное значение CRC32
adr_bit_string dd bit_string
;СЯС32-таблица для прямого табличного алгоритма вычисления CRC32
tabl_32_direct dd 256 dup (0)
len_tabl_32_direct =$-tabl_32_direct
adr_tabl_32_direct dd tabl_32_direct
polinom dd 04clldb7h
.code
:----.........расчитываем CRC32 таблицу
les di.adr_tabl_32_direct
add di.len_tabl_32_direct-4 * std ;идем назад по таблице
mov ex.255
mov ebx, polinom
ml: xor eax.eax
shrd eax.ecx.8
push ex сложенные циклы
mov ex.8
m2: shl eax.l
jnc m3 :старшие разряды неравны - выполняем сдвиг (частное нас не интересует)
:старшие разряды равны - выполняем XOR:
xor eax.ebx :ax XOR polinom
m3: loop m2
pop ex
push ex сложенные циклы
mov ex,8 m2: shl eax.l
jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует) :старшие разряды равны - выполняем XOR:
хог eax.ebx:ax XOR polinom m3: loop m2
pop сх
stosd
loop ml : закончили расчет СРО2-таблицы
mov eax. OFFFFFFFFh
Ids si,adr_bit_string
mov cx,len_bit_string m4: xor ebx.ebx
shld ebx.eax,8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
1 oop m4
xor eax. OFFFFFFFFh
;если исходная последовательность цела, то должно получиться значение crc32=9c970409h ;его можно сравнить с исходным и на этом закончить работу или продолжить до победного. :то есть до 0:
mov ex.4 : 4 (длина сгс_32) :в si адрес сгс_32
mov ebx.crc_32
bswap ebx
mov crc_32.ebx m5: xor ebx.ebx
shld ebx.eax.8
shl eax.8
xor bl.[si]
xor eax. tabl_32_direct[bx]
inc si
loop m5 :должен быть О
Заметьте, что для получения нулевого результата нам пришлось использовать команду BSWAP, чтобы «перевернуть» "значение в поле сгс_32.
Вычисление CRC
Вычисление CRC
Где начало того конца, которым оканчивается начало?
Козьма Прутков
В своей практической работе каждый пользователь наверняка сталкивался с ситуацией, когда неблагоприятные условия перемещения файлов (любым способом) приводили к порче последних. Типичное проявление этой ситуации — сообщение об ошибке при попытке чтения некоторого файла. Причина — внесенная извне техническая ошибка, приведшая к нарушению целостности исходной информации. Существует много методов для исправления подобных ошибок, но прежде чем исправлять, необходимо эти ошибки обнаружить. Для этого также существуют определенные методы, основанные на избыточности передаваемой информации, что позволяет не только выявлять наличие факта искажения информации, но и в ряде случаев устранять эти искажения. Перечислим наиболее известные из методов обнаружения ошибок передачи данных.
Посимвольный контроль четности, называемый также поперечным (Рисунок 9.1), подразумевает передачу с каждым байтом дополнительного бита, принимающего единичное значение по четному или нечетному количеству единичных битов в контролируемом байте. Может использоваться два типа контроля четности — на четность и нечетность. Алгоритм вычисления контрольного бита при контроле на четность предполагает его установку таким образом, чтобы общее количество бит в битовой последовательности (включая и сам бит четности) было четным. И наоборот, контроль на нечетность предполагает установку контрольного бита так, чтобы общее количество битов в битовой последовательности (включая и сам бит четности) было нечетным. Посимвольный контроль четности прост как в программной, так и в аппаратной реализации, но его вряд ли можно назвать эффективным методом обнаружения ошибок, так как искажение более одного бита исходной последовательности резко снижает вероятность обнаружения ошибки передачи. Этот вид контроля обычно реализуется аппаратно в устройствах связи.
Поблочный контроль четности, называемый продольным. Схема данного контроля (Рисунок 9.2) подразумевает, что для источника и приемника информации заранее известно, какое число передаваемых символов будет рассматриваться ими как единый блок данных. В этой схеме контроля для каждой позиции разрядов в символах блока (поперек блока) рассчитыва-
ются свои биты четности, которые добавляются в виде обычного символа в конец блока. При этом схема выполнения продольного контроля по-прежнему предполагает наличие у каждого из этих символов дополнительного бита четности (см. выше). По сравнению с посимвольным контролем четности поблочный контроль четности обладает большими возможностями по обнаружению и даже корректировке ошибок передачи, но все равно ему не удается обнаруживать определенные типы ошибок. Кроме того, этот вид не реализуется эффективно в аппаратных решениях, в силу чего редко используется. Главное его достоинство в том, что с него можно начинать рассмотрение идеи обнаружения ошибок на уровне блоков передаваемой информации.

Рисунок 9.1. Схема выполнения посимвольного контроля четности при передаче информации

Рисунок 9.2. Схема выполнения поблочного контроля четности при передаче информации
Вычисление контрольных сумм. В отличие от рассмотренных выше методов для метода контрольных сумм нет четкого определения алгоритма. Каждый разработчик трактует понятие контрольной суммы по-своему. В простейшем виде контрольная сумма — это арифметическая сумма двоичных значений контролируемого блока символов. Но этот метод обладает практически теми же недостатками, что и предыдущие, самый главный из которых — нечувствительность контрольной суммы к четному числу ошибок в одной колонке и самому порядку следования символов в блоке.
Контроль циклически избыточным кодом — CRC (Cyclical Redundancy Check). Это гораздо более мощный и широко используемый метод обнаружения ошибок передачи информации. Он обеспечивает обнаружение ошибок с вероятностью до 99 %. Кроме того, этот метод обладает рядом других полезных моментов, которые могут найти свое воплощение в практических задачах. Рассмотрению этого метода и будет посвящено дальнейшее изложение.
Cама по себе аббревиатура «CRC» знакома многом пользователям компьютера, особенно тем, кому приходится часто переносить свои архивные файлы посредством дискеты. В один прекрасный день попытка распаковки архивного файла наверняка приводила к выводу на экран сообщения о том, что у этого файла какое-то неправильное значение CRC. Что же представляет собой это загадочное значение CRC, какую пользу можно извлечь из знаний о нем? В данном разделе мы постараемся с этим разобраться, тем более, что данная задача является хорошей возможностью очередной раз продемонстрировать возможности и преимущества ассемблера по обработке данных на уровне битов, строк битов, последовательности байт (в том числе и неопределенной длины).
CRC (Cyclic Redundancy Code) — последовательность бит, полученная по определенному алгоритму на основании другой (исходной) битовой последовательности. Главная особенность (и практическая значимость) значения CRC состоит в том, что оно однозначно идентифицирует исходную битовую последовательность и поэтому используется в различных протоколах связи, таких, как HDLC и ZMODEM, а также для проверки целостности блоков данных, передаваемых различными устройствами. В силу этих свойств алгоритм вычисления CRC часто реализуется на аппаратном уровне. Если взять пример с архиватором, то его работа в общем случае заключается в следующем: архиватор упаковывает файлы в соответствии с некоторым алгоритмом архивации, вычисляя для каждого упаковываемого файла значение CRC. После этого заархивированные файлы могут множество раз копироваться, пересылаться по сети, в том числе с использованием электронной почты, и т. д. В процессе своих путешествий файл может столкнуться с различными неприятными воздействиями внешней среды, например, с неисправным дисководом, искажением его внутреннего содержимого во время передачи по сети и т. п. Эти изменения не обязательно должны быть глобальными, они могут касаться всего одного бита. Когда приходит время, пользователь распаковывает архив, при этом архиватор в первую очередь проверяет целостность файлов в нем. Для этого архиватор опять по содержимому файла вычисляет его CRC и сравнивает полученное значение с тем значением CRC, которое было вычислено при упаковке файла. Если они равны, то считается, что целостность файла не была нарушена, и он распаковывается, в обратном случае, если новое и старое значения CRC не совпадают, то считается, что архивный файл поврежден, и процесс его распаковки завершается. Необходимо отметить, что CRC не обязательно вычислять для больших массивов данных, каким является файл. Его можно вычислять и для отдельных строк текста и даже слов с целью организации простейшего контроля целостности и отождествления символьных (числовых) последовательностей. Более того, из рассмотрения ниже вы увидите, что алгоритм вычисления CRC, по сути, является еще одним методом хэширования, которые мы подробно рассматривали в разделе «Таблицы с вычисляемыми входами» главы 2. Таким образом, алгоритм вычисления CRC имеет много досто-
инств, которые могут найти применение в самых различных практических задачах.
Основная идея вычисления CRC заключается в следующем. Исходная последовательность байтов, которой могут быть и огромный файл, и текст размером несколько слов и даже символов, представляется единой последовательностью битов. Эта последовательность делится на некоторое фиксированное двоичное число. Интерес представляет остаток от этого деления, который и является значением CRC. Все, что теперь требуется, — это некоторым образом запомнить его и передать вместе с исходной последовательностью. Приемник данной информации всегда может таким же образом выполнить деление и сравнить его остаток с исходным значением CRC. Если они равны, то считается, что исходное сообщение не повреждено, и т. д. Но этот лишь общая схема. Реальный алгоритм вычисления CRC использует особые правила арифметики, в соответствии с которыми производятся все вычисления, назовем их правилами CRC-арифметики. В силу принципиальной важности этих правил для нашего изложения коротко рассмотрим их отличия от правил обычной двоичной арифметики.
В заключение данного раздела обсудим
«Зеркальный» табличный алгоритм CRC32
В заключение данного раздела обсудим «зеркальный» вариант табличного алгоритма — алгоритм CRC32 (V.42 МККТТ). Этот вариант вычисления CRC обязан своим возникновением существованию последовательного интерфейса, который посылает биты, начиная с наименее значимого (бит 0) и заканчивая самым старшим (бит 7), то есть в обратном порядке. В «зеркальном» регистре все биты отражены относительно центра. Например, 10111011001 есть отражение значения 10011011101.
Вместо того чтобы менять местами биты перед их обработкой, можно зеркально отразить все значения и действия, участвующие в прямом алгоритме. При этом
направление расчетов поменяется — байты теперь будут сдвигаться вправо, полином 04clldb7h зеркально отразится относительно его центра, в результате получится значение 0edb88320h. С11С32-таблица будет зеркальным отражением аналогичной таблицы для прямого алгоритма (Рисунок 9.10).

Рисунок 9.10. Схема «Зеркального» табличного алгоритма
Для зеркального алгоритма вычисления CRC32 процесс вычисления такой же, за исключением порядка — сдвиги и заполнение регистра осуществляются вправо. Ниже приведена программа вычисления таблицы для зеркального алгоритма CRC32 и полинома 0EDB88320h.
;prg09_08.asm - программа вычисления таблицы для зеркального алгоритма CRC32 :и полинома 0EDB88320h
.data
:СРС32-таблица для зеркального табличного алгоритма вычисления CRC32
tabl_32_mirror dd 256 dup (0)
len_tabl_32jrrirror=$-tabl_32_mirror
adr_tabl_32jTrirror dd tabl_32_mirror
polinom dd 0EDB88320h
.code
les di.adr_tabl_32_mirror
add di,len_tabl_32_mirror-4
std ;идем назад по таблице
mov ex.255
mov ebx.polinom
ml: xor eax.eax
mov al.cl ;индекс в таблице для вычисления CRC
push ex сложенные циклы
mov ex.8
m2: shr eax.l
jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует)
;старшие разряды равны - выполняем XOR:
xor eax.ebx:ax XOR polinom
m3: loop m2
pop ex stosd
loop ml
Для того, кто обладает солидным багажом знаний по проблеме CRC-вычис-лений, написание программы, реализующей зеркальный алгоритм, — дело техники. На стороне источника код будет выглядеть так:
;prgO9_O9.asm - программа вычисления кода CRC32 на стороне источника :для зеркального алгоритма CRC32 и полинома 0EDB88320h.
.data
исходная битовая последовательность в символах bit_stnng db "123456789" 1en_bi t_string=$-bi t_string
crc_32 dd 0 :сюда мы поместим рассчитанное значение CRC32 adr_bit_string dd bit_string
:СРС32-таблица для зеркального табличного алгоритма вычисления CRC32 .. tab1_32_mirror dd 256 dup (0) len_tabl_32_mirror=$-tabl_32_mirror adr_tabl_32_mirror dd tabl_32_mirror polinom dd 0EDB88320h .code
:-------......расчитываем зеркальную СКС32-таблицу.........
les di.adr_tabl_32_mirror
add di,len_tabl_32_mirror-4
std :идем назад по таблице
mov ex.255
mov ebx.polinom
ml: xor eax.eax
mov al.cl ;индекс в таблице для вычисления CRC
push ex ;вложенные циклы
mov ex.8
m2: shr eax.l
jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует) :старшие разряды равны - выполняем XOR:
xor eax.ebx:ax XOR polinom
m3: loop m2
pop сх
stosd ' '
loop ml закончили расчет СРС32-таблицы
xor bx.bx
mov eax. OFFFFFFFFh
Ids si,adr_bit_string
mov cx,len_bit_string
m4: mov Ы .al
shr eax.8
xor bl.[si]
xor eax.tabl_32_mirror[bx]
inc si
1 oop m4
xor eax. OFFFFFFFFh ;запишем сгс-32 в конец последовательности:
mov сгс_32.еах добавляем в конец исходной последовательности
Для исходной строки "123456789" получили CRC=lb948a57h. Теперь осталось приемнику проверить целостность полученной им строки. Приемник работает по второму варианту и выполняет действия, иллюстрируемые следующей программой. Если полученная им строка совпадает с исходной, то результатом работы программы должно быть значение 6b202ca2h.
:prg09_10.asm - программа вычисления кода CRC32 на стороне приемника ;для зеркального алгоритма CRC32 и полинома 0EDB88320h.
1
:исходная битовая последовательность в символах
bit_string db "123456789"
1en_bit_string=$-bit_string
сгс_32 dd Ib948a57h :сюда мы поместили рассчитанное значение CRC32
adr_bit_string dd bit_string
:С(}С32- таблица для зеркального табличного алгоритма вычисления CRC32
tabl_32_mirror dd 256 dup (0)
1 en_tabl_32_mi rror=$-tabl_32_nii rror
adr_tabl_32_mirror dd tabl_32_mirror
polinom dd 0EDB88320h
.code
:.........
;----........расчитываем зеркальную CRC32-Ta6flnuy.........
les di,adr_tabl_32_mirror
add di,len_tabl_32_mirror-4
std ;идем назад по таблице
mov ex.255
mov ebx.poli nom ml: xor eax.eax
mov al.cl :индекс в таблице для вычисления CRC
push сх сложенные циклы
mov сх,8 m2: shr eax.l
jnc m3 ;старшие разряды не равны - выполняем сдвиг (частное нас не интересует) :старшие разряды равны - выполняем XOR: * xor eax,ebx:ax XOR polinom m3: loop m2
pop ex
stosd
loop ml закончили расчет (Ж32-таблицы
xor bx.bx
mov eax. OFFFFFFFFh
Ids si.adr_bit_string
mov cx.len_bit_string+4 ;4 - длина crc_32 m4: mov bl.al
shr eax.8
xor bl.[si]
xor eax.tabl_32_mirror[bx]
inc si loop m4 :сравнить - результат должен быть константой 6b202ca2h
Этот вариант работы алгоритма вычисления CRC32 удобен тем, что не нужно знать длину собственно исходной последовательности (без значения CRC). Достаточно просто обработать весь входной поток, не различая в строке завершающую ее подстроку с CRC. Далее необходимо сравнить содержимое регистра ЕАХ с 6b202ca2h. Если эти значения равны, значит, исходная последовательность нарушена не была. Для получения собственно строки достаточно отбросить последние 4 байта сообщения, полученного приемником. И последнее замечание, которое говорит о том, что проблема вычисления CRC неоднозначна для понимания и предоставляет большое поле для проведения различных экспериментов и совершенствования существующих алгоритмов. Небольшой поправкой в алгоритме работы источника можно сделать так, что успехом целостности при принятии приемником сообщения может быть не указанная выше константа, а нуль. Для этого источнику достаточно не объединять вычисленное значение CRC32 по XOR с Offffffffh, а просто добавить его к исходной последовательности. Оба эти варианта хороши тем, что не нужно заранее знать длину анализируемого сообщения.
На этом, пожалуй, можно и закончить обсуждение проблемы вычисления CRC. На примере этой достаточно сложной задачи были в очередной раз продемонстрированы варианты использования средств ассемблера для обработки информации на различных уровнях, вплоть до битового. За дальнейшими подробностями по проблематике вычисления CRC обратитесь к соответствующим источникам.