Программирование ХММ-расширения

Что бы ученые ни придумали, отвечать приходится студенту.
А. Хлудеев

В этой главе мы рассмотрим практические вопросы программирования ХММ-расширения микропроцессора Pentium III. Программирование целочисленного MMX-расширения рассмотрено в уроке 20 «ММХ-технология микропроцессоров Intel» учебника. Там же рассмотрены архитектура и система команд ХММ-расширения, но остались «за бортом» вопросы организации практической работы с ними. Кроме учебника архитектура и система команд ХММ-расширения рассмотрены в литературе.
С точки зрения структуры материал, изложенный ниже, состоит из двух частей: в первой части рассматриваются практические аспекты применения команд ХММ-расширения для решения некоторых типов задач, а во второй части — порядок разработки программ, использующих команды ХММ-расширения. Предполагается, что для разработки ассемблерных программ используется пакет TASM.

Программирование ХММ-расширения

Новые сапоги всегда жмут.
Козьма Прутков

Необходимо отметить тот факт, что фирма Intel — не единственная из фирм, разрабатывающих микропроцессоры, активно работает над проблемой обработки больших массивов однородной информации. Не секрет, что постоянным соперником фирмы Intel по вопросам архитектуры микропроцессора является фирма AMD. Между ними по различным направлениям идет постоянная борьба за рынок компьютеров архитектуры х86. Мы не будем рассматривать ее хронологию, уделим внимание лишь тому, для чего и в какой форме в архитектуре микропроцессоров этих фирм появились средства для потоковой обработки данных с плавающей точкой или SSE (Streaming SIMD Extensions). Толчком к развитию SIMD-технологий (в том числе и целочисленных) стали задачи с большими объемами однородных исходных данных простой структуры. Основные области, где встречается такая информация, — Интернет и компьютерные игры. Именно здесь возникает множество задач по обработке звука, видео, графики. Если рассматривать современные компьютерные игры, то в них активно используются мощности со-
процессора для производства расчетов ЗО-объектов в трехмерном пространстве (отсюда, кстати, и название — 3DNow!). Архитектура и производительность стандартного сопроцессора не обеспечивают с нужной эффективностью эти расчеты. Фирмы — производители микропроцессоров активно начали поиск технологий, которые позволили бы увеличить производительность подсистемы для расчетов с плавающей точкой. Известно несколько путей повышения эффективности расчетов подобного рода: увеличение тактовой частоты, уменьшение задержек выполнения команд в сопроцессоре, конвейеризация вычислений с плавающей точкой, реализация SIMD-технологии, использование параллельных конвейерных устройств для расчетов с плавающей точкой. Среди этих путей фирмы Intel и AMD выбрали свои. Тактовую частоту работы микропроцессора постоянно повышают обе фирмы, чему мы являемся заинтересованными свидетелями. Что же касается подсистемы обработки данных с плавающей точкой, то архитектурно они реализованы по-разному. Так, фирма Intel пошла по пути конвейеризации вычислений с плавающей точкой и реализации SIMD-технологии вычислений с плавающей точкой. Фирма AMD работает над уменьшением задержек выполнения команд в сопроцессоре и над реализацией SIMD-технологии вычислений с плавающей точкой. Эти технологии реализованы в микропроцессорах Pentium III фирмы Intel и Atlon фирмы AMD, но они не совсем одинаковы. Архитектура целочисленного MMX-расширения у этих микропроцессоров совпадает (в семействе AMD целочисленное MMX-расширение появилось в микропроцессоре AMD Кб (ММХ)), что же касается архитектуры ХММ-расширения с плавающей точкой, то здесь различия более существенные начиная с их названий. Потоковое расширение с плавающей точкой микропроцессора Atlon называется 3DNo\v! и включает 21+5 команд. 21 команда расширения 3DNow! существовала в предыдущем микропроцессоре AMD K6-2-3DNow!, 5 команд этого расширения были введены дополнительно в расширение 3DNow! микропроцессора AMD Athlon. Потоковое расширение микропроцессора Pentium III фирмы Intel называется Streaming SIMD Extensions и включает 70 команд. Стоит отметить, что не все из этих 70 команд являются командами SSE-расширения: 50 команд относятся непосредственно к блоку SSE-расширения, то есть являются командами SIMD с плавающей точкой, 12 команд дополняют систему команд целочисленного MMX-расширения и 8 команд относятся к системе кэширования.
Велики различия в физической реализации расширений 3DNow! и Streaming SIMD Extensions. SSE-расширение фирмы Intel выполнено в виде отдельного блока, расширение 3DNow процессоров AMD реализовано на базе стандартного сопроцессора. Второе важное отличие — размерность регистров. Их количество совпадает для обоих расширений. Размерность регистров SSE-расширения — 128 бит, то есть 4x32 бита в формате короткого слова с плавающей точкой. Размерность регистров расширения 3DNow — 64 бита, то есть 2x32 бита в формате короткого слова с плавающей точкой. Таким образом, SSE-расширение процессоров Intel имеет вдвое больше регистров, чем 3DNow!-pacurapeHne процессоров AMD. Выводы из этого делайте сами. К примеру, задачи трехмерной графики активно работают с матрицами 4x4 (см. ниже). В процессе написания программы для 3DNow!-pacnrapeHra процессора AMD пропэаммист вынужден постоянно решать проблему нехватки регистров в 3DNow! со всеми вытекающими последствиями, в том числе и для красоты алгоритма. Реализация SSE-расширения
в виде отдельного блока увеличивает параллельность вычислений в процессоре, так как одновременно могут выполняться команды целочисленного устройства, сопроцессора и SSE-расширения. Читатель может возразить, что, несмотря на все эти недостатки, результаты тестов в различных изданиях говорят о том, что зачастую не наблюдается существенного различия в производительности микропроцессоров фирм Intel и AMD одного класса. На взгляд автора, это следствие I того, что фирме AMD удается компенсировать существующие архитектурные различия хорошей проработкой схемотехнических проблем микроархитектурного уровня. Дальнейшее изложение будет основано на базе ХММ-расширения Pentium III — то есть SSE-расширения.
Наибольшую выгоду от использования SSE-расширения Pentium получают задачи трехмерной графики, а также приложения 2D- и 2.50-графики, использующие векторную графику в фоновой части изображения. При желании программист может найти полезные особенности команд ХММ-расширения для использования их при разработке приложений из других предметных областей. Один из основных признаков, на которые стоит обратить внимание при выборе средств реализации, — наличие матричных преобразований, таких как умножение, транспонирование, сложение, вычитание матриц, умножение матрицы на вектор, световые преобразования, подобные преобразованиям между цветовыми моделями RGB и CMYK, и т. п.
В заключение этой части обсуждения отметим, что набор SIMD-инструкций ХММ-расширениия микропроцессора Intel (и AMD тоже) бесполезен без соответствующей программной поддержки. Далее рассмотрим, каким образом использовать ХММ-команды в программах на языке ассемблера. Следует отметить, что данный материал может быть полезен не только для программистов на языке ассемблера, но и для тех, кто пишет программу на языке высокого уровня. Благодаря ассемблерным вставкам или внешним ассемблерным процедурам программист может использовать возможности новых процессоров, не дожидаясь появления новой версии компилятора, поддерживающего эти возможности. Это также имеет место с Pentium III. Оперативно отслеживать процессорные новшества удается только компилятору С/С ++ фирмы Intel и макроассемблеру фирмы Microsoft, который поддерживает новые команды SSE начиная с версии 6.1 Id и выше. Но известно, что далеко не все программисты на С и ассемблере предпочитают эти компиляторы другим аналогичным средствам разработки. Что же делать таким программистам, в частности программирующим на ассемблере с использованием пакета TASM? Ответ один — выкручиваться. Как? Этому и будет посвя-гцено обсуждение ниже. Оно будет логически состоять из двух частей. В первой части мы сделаем вид, что ничего не происходит и транслятор TASM поддерживает любые команды процессора Pentium III. Во второй части мы действительно поможем TASM это сделать.
Вначале разберем порядок описания данных, которыми манипулируют ХММ-команды Pentium III, а затем рассмотрим несколько примеров их использования.

Описание упакованных и скалярных данных

Описание ХММ-данных в приложении обычно производится в одном из двух форматов:

в массиве структур;

в структуре, элементами которой являются массивы.

Описание точек изображения в трехмерном пространстве принято задавать в виде четырехмерного вектора (x.y.z.w). Это связано с тем, что проективные преобразования, необходимые для показа изображения с различных точек зрения, наиболее просто описываются матрицами 4x4. Используя перечисленные выше форматы задания ХММ-данных, совокупность точек в трехмерном пространстве можно описать двумя способами:

первый способ — для каждой точки определить свой экземпляр структуры:
point 3D struc х del 0.0 у dd 0.0 z dd 0.0 w dd 0.0
ends .data pi point_3D 4 dup (<>) ;описание пирамиды массивом структур.
;каждая из которых описывает одну из 4 вершин В второй способ — все точки описать одной структурой, элементами которой являются массивы координат x,y,z,w:
pri sm_point_3Dstruc x dd 4 dup (0.0) у dd 4 dup (0.0) z dd 4 dup (0.0) w dd 4 dup (0.0)
ends .data prism prism_point_3D<> структура, описывающая треугольную пирамиду (4 вершины)

Приведенные выше примеры описания пирамиды иллюстрирует рис. 10.1.

Рис. 10.1. Расположение в памяти описания вершин пирамиды

В большинстве приложений используется первый способ представления ХММ-данных, хотя он считается и менее эффективным. При необходимости можно произвести преобразование представления данных из одного способа в другой. Вариант такого преобразования показан в программе ниже.

;рrg10 01.asm - программа преобразования представления ХММ-данных :из одного способа представления в другой.
prizm struc
union
struc структура, описывающая треугольную пирамиду (1 способ)
xyzwl dd 0.0
xyzw2 dd 0.0
xyzw3 dd 0.0
xyzw4 dd 0.0
ends
struc структура, описывающая треугольную пирамиду (2 способ) х dd 4 dup (0.0) у dd 4 dup (0.0) z dd 4 dup (0.0) w dd 4 dup (0.0)
ends
ends ;конец объединения
ends .data
prizm_l prizm <> :экземпляр объединения .code
преобразование представлений вершин пирамиды (на месте)
lea si.prizm_l
movlps rxmm0.[si] ;rxmm0=? ? уО xO
movhps rxmmO,[si+16] ;rxmm0= yl xl yO xO
movlps rxmm2.[si+32] ;rxmm2« ? ? y2 x2
movhps rxmm2.[si+48] ;rxmm2= уЗ хЗ у2 х2
movaps rxmml.rxmmO :rxmml= yl xl yO xO
shufps rxmmO.rxmm2.88h :rxmm0= x3 x2 xl xO
shufps rxmml.rxmm2.0ddh ;rxmml= уЗ у2 yl yO
movlps rxmm2.[si+8] ;rxmm2=? ? wO zO
movhps rxmm2.[si+24] :rxmm2= wl zl wO zO
movlps rxmm4.[si+40] ;rxmm4= ? ? w2 z2
movhps rxmm4,[si+56] ;rxmm4= w3 z3 w2 z2
movaps rxmm3.rxmm2 ;rxmm3= wl zl wO zO
shufps rxmm2.rxmm4.88h :rxmm2= = z3 z2 zl zO
shufps rxmm3.rxmm4.0ddh ;rxmm3= w3 w2 wl wO . -на выходе получим следующее состояние ХММ-регистров:
;RXMM0= хЗ х2 xl xO. RXMM1= уЗ у2 yl yO. RXMM2= ¦ z3 z2 zl zO. RXMM3= w3 w2 wl wO :теперь их необходимо сохранить в памяти:
movups [si].rxmm0
movups [si+16].rxmml
movups [si+32].rxmm2
movups [si+48].rxmm3

Описание скалярных данных намного проще - это обычные значения с плавающей точкой в коротком формате:

.data
seal real dd 1.0 :пример описания скалярного ХММ-значения;

Примеры использования команд ХММ-расширения

Ниже будут рассмотрены несколько типовых примеров использования команд ХММ-расширения. Основная цель — демонстрация методики работы с основными группами команд ХММ-расширения. Начнем с реализации простейших операций — сложения и умножения.

Сложение и умножение двух упакованных ХММ-значений

Задача — вычислить скалярное произведение двух векторов, каждый из которых состоит из 4 вещественных чисел в коротком формате. Если в качестве таких векторов взять два вектора А и В, то их произведение вычисляется по формуле: АхВ = aoxbo+aixbi+a2xb2+a3xb3- В программной реализации с использованием ХММ-команд это выглядит так, как показано ниже.

:prg10_02.asm - программа вычисления скалярного произведения двух векторов.
.data
xmm_pack_l dd 1.0. 2.0. 3.0. 4.0
xmm_pack_2 dd 5.0. 6.0. 7.0. 8.0
rez_sum dd 0.0 результат сложения .
.code
movaps rxmmO.xrom_pack_l ;RXMM0= 4.0. 3.0, 2.0, 1.0 mulps rxmm0.xinTi_pack_2 :RXMM0= 4.0x8.0. 3.0x7.0. 2.0x6.0, 1.0x5.0 movaps rxmml. rxmmO :RXMM1= 4.0x8.0, 3.0x7.0. 2.0x6.0. 1.0x5.0
shufps rxmml.rxmml.4eh ;RXMM1= 2.0x6.0, 1.0x5.0. 4.0x8.0. 3.0x7.0 addps rxmmO. rxmml :складываем:
;RXMM0= 4.0x8.0. 3.0x7.0. 2.0x6.0, 1.0x5.0
J +
:RXMM1= 2.0x6.0. 1.0x5.0. 4.0x8.0. 3.0x7.0
:RXMM0- 4.0x8.0+2.0x6.0. 3.0x7.0+1.0x5.0, 2.0x6.0+4.0x8.0. 1.0x5.0+3.0x7.0
:или
;RXMM0= 44.0. 26.0, 44.0. 26.0
movaps rxmml, rxmmO :RXMM1= 44.0, 26.0, 44.0, 26.0
shufps rxmml.rxmml.llh :RXMM1= 26,0. 44.0. 26.0. 44.0
addps rxmmO. rxmml :складываем: ;RXMM0= 44.0. 26.0. 44.0, 26.0
; +
;RXMM1= 26.0, 44.0, 26.0, 44.0
:RXMM0= 70.0. 70.0, 70.0, 70.0 сохраняем результат movss rez_sum.rxmm0

Умножение матрицы на вектор

Умножение матрицы на вектор — наиболее характерная операция для вычислений в области машинной графики. Существуют различные способы формирования трехмерного изображения. В наиболее простом случае изображение на экране задается в виде опорных точек. К примеру, рассмотрим случай, когда на экране дисплея находится трехмерное изображение, состоящее из отрезков прямых. Необходимая для его формирования информация хранится в памяти как список опорных точек — концов отрезков. Если изображение дается в трехмерном изображении, то описание каждой точки удобно задать в виде четырехмерного вектора (х, у, z, w). Включение в трехмерный вектор (х, у, z) дополнительной координаты w объясняется тем, что проективные преобразования, необходимые для показа изображения с различных точек зрения, описываются матрицами 4x4. Поэтому для удобства реализации проективных преобразований, зачастую сопровождаемых операциями умножения матриц и векторов, трехмерный вектор (х, у, z) представляют в виде четырехмерного вектора (х, у, г, w), где значение w обычно принимается равным 1. Для выполнения самого преобразования, подготовленная заранее матрица преобразования умножается на этот вектор, в результате чего получается четырехмерный вектор (х1, у', г , w'). Для обратного перехода к требуемому трехмерному вектору необходимо разделить координаты х', у', г на w', после чего удалить четвертую координату w'.
Матрица М преобразования и вектор V имеют следующий вид:

m00 m01 m02 m03 x
mio mu m12 m13 у
m20 m21 m22 m23 z
m30 m31 m32 m33 w=l

Преобразования координат выполняются по формулам:

х' ™ xxm0o+yxni01+zxm02+lxm03
у' » xxm+yxnid+zxm+lxm
г = xxm20+yxm21+zxm22+lxm23
w' = xxm30 +yxm31+zxm32+lxm33

Для получения преобразованных координат в виде трехмерного вектора (x,y,z) делим х', у', z' на w':

х = x'/w' = (ххт00+ухт01+гхт02+1хт0з)/(ххт30+ухт31+гхт32+1хт3з)
У = У'/w' = (xxmlo+yxm))+zxm,2+lxm13)/(xxm3O+yxm31+zxm32+lxm33)
z - z'/w' = (xxm20+yxm2i+zxm22+lxm23)/(xxm30+yxm31+zxm32+lxm33)

Элементы матрицы И векторов представлены числами с плавающей точкой в коротком вещественном формате (4 байта).
Ниже приведены два варианта программы умножения матрицы на вектор — один с использованием стандартного сопроцессора, другой с использованием команд ХММ-расширения (с помощью профайлера можно сравнить скорость преобразования). Результирующий трехмерный вектор замещает исходный.

Умножение матрицы 4x4 на четырехмерный вектор (стандартный сопроцессор)

Подпрограмма состоит из двух частей. В первой части вычисляется собственно произведение четырехмерной матрицы на четырехмерный вектор. Во второй части полученный четырехмерный вектор преобразуется влрехмерный путем деления его компонентов на его четвертую координату.

:prgl0_05.asm - программа поворота изображения на месте :с использованием средств стандартного сопроцессора.
t :
:координаты квадрата (необходимо инициализировать) xO.yO.xl.yl.x2.y2.x3.y3 mas_xy dd 8 dup (0.0)
a dd 0.0 :угсл (необходимо инициализировать) .code
lea si.mas_xy
mov ex.4 :цикл 4 раза - по количеству вершин
firm ;вычисляем sin а и cos a;
fid a ;включаем а стек угол
fsin вычисляем sin a
fxch ;меняеи st(0)<->st(l)
fcos ;вычисляем cos a
fxch ;меняем st(0)<->st(l)
fstp a :выталкиваем а :поворот изображения cycl: fild word ptr [si] :включить в стек координату х элемента
fild word ptr [si+2] :включить в стек координату у элемента
fid St(l) ;дублируем их
fid st(l)
fmul st.st(5) вычислить y*sin
fxch :меняем st(0)<->st(l)
fmul St.st(4) вычислить x'cos
fadd :новая координата х
fistp word ptr[si] :передать новую координату х в память
fmul st.st(2) вычислить y*cos
fxch ' ;меняем st(0)<->st(l)
fmul St.StO) .-вычислить x*sin
fsubr .новая координата у
fistp word ptr[si*4] ;передать ее в память
add si.8 ;продвинуть указатель массива mas_xy
loop cycl повторить еще 3 раза :в mas_.ху преобразованные для поворота координаты квадрата
Поворот изображения (ХММ-расширение)
:prgl0_06.asm - программа поворота изображения на месте
:с использованием средств ХММ-расширения.
.data
:ALIGN 16
:координаты квадрата (необходимо инициализировать) хО,уО,х1.у1.х2.у2.х3.уЗ
mas_xy dd 8 dup (0.0)
a dd 0.0 :угол (необходимо инициализировать)
sin_a dd 0.0
cos_a dd 0.0
null dd 0.0
. code
:.........

lea esi.raas_xy
mov ecx.4 :цикл 4 раза - no количеству вершин
finit вычисляем sin а и cos a;
fid a :включаем в стек угол
fsin вычисляем sin a
fxch ;меияем st(Q)<->st(l)
fcos ;вычисляем cos a
fxch ;меняем st(0)<->st(l;
fstp a ;выталкиваем а
fstp cos_a ; выталкиваем cos__a
fstp sin_a ;выталкиваем sin_a
;поворот изображения
;готовим xmm-регистр RXMM2 со значениями углов movlps rxmm2.sin_a
movhps rxmm2,sin_a ;RXMM2= cos_a sin_a cos_a sin__a
movss rxmm2.nul1
siibss rxmm2.sin_a ;RXMM2= cos_a sin_a cos_a -sin_a
cycl: movlps rxmmO.Lesi] :RXMM0= ? ? yi xi movhps rxnwO.Cesi] ;RXMM0= yi xi yi xi
shufps rxmmO.rxmmO.ObOh :RXMM0= xi yi yi xi
mulps rxmmO.rxnm2 ;RXMM0-RXMM0*RXMM2= xi*cos_a yi*sin_a yi* cos_a xi*(-sin_a)
shufps rxmml.rxmmO.31h ;RXMM1=? xi*cos_a ? yi* cos_a
addps rxmmO.rxmml :RXMM0= ? (xi*cos_a+yi*sin_a) ? (yi* cos_a+xi*(-sin_a))
shufps rxmmO.rxmmO.2 ;RXMM0=- ? ? (yi* cos_a+xi*(-sin_a)) (xi*cos_a+yi*sin_a) сохраняем результат: movlps [esi].rxnim0 ;готовимся к вычислению нового положения для следующей координаты
add esi,8 1oop cycl

На этом мы закончим рассмотрение примеров программирования ХММ-расширения. При разработке приведенных выше программ мы считали, что используемый нами транслятор ассемблера поддерживает любые команды микропроцессора Intel, в том числе и ХММ-команды. Реально ситуация далека от этой идеальной картины. Мы уже упоминали, что если транслятор MASM (фирмы Microsoft) пытается поспевать за процессом развития системы команд, то для TASM дело обстоит несколько хуже. Другие фирмы-разработчики трансляторов ассемблера мы не рассматриваем (не потому, что они хуже — просто обсуждение достоинств и недостатков трансляторов ассемблера не является предметом данной книги). Настало время, не меняя любимого транслятора, помочь ему понять неизвестные команды микропроцессора. Для этого в следующей части данного раздела мы выработаем соответствующую методику.

Препроцессор команд ХММ-расширения

Отыщи всему начало, и ты многое поймешь.
Козьма Прутков

Задачу адаптации транслятора TASM к новым командам микропроцессора, и в частности к ХММ-командам, можно решить двумя способами.

Можно разработать включаемый файл, в котором дляя каждой ХММ-ком ды реализовать макрокоманду, моделирующую на ббазе существующих к манд нужную ХММ-команду. Кроме этого, фирма Irintel, зная об инерцио ности процесса разработки новых версий трансляторров ассемблера, вмест с подмножеством новых команд разрабатывает соотгветствующий включа мый файл для их поддержки в ассемблерных прогрэаммах. Для подмножества ХММ-команд такой файл называется iaxmm.inac. Он ориентирован на транслятор MASM (фирмы Microsoft) и не пригодеен (требует доработки") для TASM. Однако при доработке TASM необходимую иметь в виду вопрос об авторских правах. Некоторые проблемы использоования файла iaxmm.inc совместно с TASM обсуждены ниже. Можно разработать программу-препроцессор, на ввход которой подавать исходный файл с программой на ассемблере, содеряжащей новые команды процессора, а на выходе получать текст, адаптированнный для компиляции старым транслятором ассемблера. Этот путь имеет' то преимущество, что теперь при появлении новых команд можно, не вноося больших корректив в технологию разработки программ, всего лишь орпределенным образом модифицировать файл-препроцессор, дополнив его i возможностями по обработке новых команд процессора. Более того, дополяяив препроцессор средствами распознавания микропроцессора (Intel или /AMD), можно разрабатывать программы с использованием расширения 31DNo\v!.

Первый способ был реализован в уроке «ММХ-техномюгия микропроцессоров Intel» учебника для ММХ-команд. Там же были привзедены примеры включаемых файлов, полностью пригодных для использованияя как 16-, так и 32-разрядными приложениями на ассемблере. Поэтому основносе внимание мы уделим второму способу организации поддержки ХММ-команд — препроцессорному. Но вначале рассмотрим структуру и содержание включаеемого файла iaxmm.inc. Текст этого файла можно загрузить с официального сайта компании Intel (http:// www.intel.com).

Поддержка ХММ-команд в файле iaxmm.inc

С точки зрения структуры включаемый файл iaxmm.inc представляет собой набор макрокоманд двух типов — основных и вспомогательньях. Названия основных макрокоманд полностью совпадают с названиями ХММ-команд, и эти макрокоманды обеспечивают моделирование определенных XlMM-команд. Вспомогательные макрокоманды расположены в начале файла и предназначены для обеспечения работы основных макрокоманд. В частности, :эти макрокоманды устанавливают тип операндов, указанных при обращении к (основной макрокоманде, причем делают это исходя из режима функционировашия транслятора — 16-или 32-разрядного. Другое важное действие — установление соответствия между названиями ХММ-регистров и регистров общего назначения. Дело в том, что для моделирования ХММ-команд в 16- или 32-разрядном режиме работы ассемблера используются разные регистры общего назначения — 1 6-разрядные регистры в 16-разрядном режиме, и 32-разрядные в 32-разрядном режиме.
Рассмотрим процесс моделирования ХММ-команд. В! качестве основы для моделирования выступает команда основного процессора!. Эта команда должнаудовлетворять определенным требованиям. Каковы они? В поисках ответа посмотрим на машинные коды ХММ-команд в литературе [40, 41]. Видно, что общими у них являются два момента:

поле кода операции ХММ-команд состоит из двух или трех байтов, один
из которых равен Ofh; большинство ХММ-команд использует форматы адресации с байтами modR/M и sib и соответственно допускает сочетание операндов как обычных двух-операндных команд целочисленного устройства — регистр-регистр или память-регистр.

Для моделирования ХММ-команд нужно подобрать такую команду основного процессора, которая удовлетворяет этим двум условиям. Во включаемом файле iaxmm.inc в качестве таких команды присутствуют две — CMPXCHG и ADD. В процессе моделирования на место нужного байта кода операции этих команд помещаются байты со значениями кода операции соответствующей ХММ-команды. Когда микропроцессор «видит», что очередная команда является ХММ-командой, то он начинает трактовать коды регистров в машинной команде как коды ХММ-регистров и ссылки на память, размерностью соответствующей данной команде. В машинном формате команды нет символических названий регистров, которыми мы пользуемся при написании исходного текста программы, например АХ или ВХ. В этом формате они определенным образом кодируются. Например, регистр АХ кодируется в поле REG машинной команды как 000. Если заменить код операции команды, в которой одним из операндов является регистр АХ, на код операции некоторой ХММ-команды, то это же значение в поле reg микропроцессор будет трактовать как регистр RXMMO. Таким образом, в ХММ-командах коды регистров воспринимаются соответственно коду операции. В табл. 10.1 приведены коды регистров общего назначения и соответствующих им ХММ-регистров. В правом столбце этой таблицы содержится условное обозначение ХММ-регистров, принятое в файле iaxmm.inc. Это же соответствие закреплено рядом определений в этом файле, которые иллюстрирует следующая программа.

DefineXMMxRegs Macro IFDEF APPJ.6BIT
rxmmO TEXTEQU<AX>
rxmml TEXTEQU<CX>
rxmm2 TEXTEQU<DX>
rxmm3 TEXTEQU<BX>
rxmm4 TEXTEQU<SP>
rxmm5 TEXTEQU<BP>
гхттб TEXTEQU<SI>
rxmm7 TEXTEQU<DI>
RXMMO TEXTEQU<AX>
RXMM1 TEXTEQU<CX>
RXMM2 TEXTEQU<DX>
RXMM3 TEXTEQU<BX>
RXMM4 TEXTEQU<SP>
RXMM5 TEXTEQU<BP>
P.XMM6 TEXTEQU<SI>
RXMM7 TEXTEQU<DI>
rxmml TEXTEQU<ECX>
rxmm2 TEXTEQU<EDX>
rxmm3 TEXTEQU<EBX>
rxmm4 TEXTEQU<ESP>
rxmm5 TEXTEQU<EBP>
гхттб TEXTEQU<ESI>
ГХШП7 TEXTEQU<EDI>
RXMMO TEXTEQU<EAX>
RXMM1 TEXTEQU<ECX>
NRXMM2 TEXTEQU<EDX>
RXMM3 TEXTEQU<EBX>
RXMM4 TEXTEQU<ESP>
RXMM5 TEXTEQU<EBP>
RXMM6 TEXTEQU<ESI>
RXMM7 TEXTEQU<EDI> ENDIF endm

Таблица 10.1. Кодировка регистров в машинном коде команды

Код в поле reg	Регистр целочисленного устройства	ХММ-регистр
000	АХ/ЕАХ	RXMM0
001	СХ/ЕСХ	RXMM1
010	DX/EDX	RXMM2
Oil	ВХ/ЕВХ	RXMM3
100	SP/ESP	RXMM4
101	ВР/ЕВР	RXMM5
110	SI/ESI	RXMM6
111	DI/EDI	RXMM7

Теперь в исходном тексте программы можно использовать символические имена ХММ-регистров в качестве аргументов макрокоманд, моделирующих ХММ-команды.
Рассмотрим, как в файле iammx.inc описано макроопределение для моделирования ХММ-команды скалярной пересылки MOVSS.

:F3 OF 10 /г movss xrrnil. xmm2/m32 :F3 OF 11 /r movss xmm2/m32. xnrnl movss macro dst:req. src:req
XMMld_st_f3 opc_Mo«s. dst, src endm

Понимание структуры приведенного макроопределения не должно вызвать у читателя трудностей. Начать следует с того, что данная команда содержит вложенный вызов макрокоманды XMMld_st_f3, у которой две задачи — определить вариант сочетания операндов, после чего сформировать правильный код операции и подставить его на место соответствующих байтов в команде CMPXCHG. В результате этих действий команда CMPXCHG «превращается» в ХММ-команду MOVSS.

1. XMMld_St f3 macro op:req.dst:req, src:req
2. local x. у
3. Defin'eXMMxRegs
4. IF (OPATTR(dst)) AND OOOlOOOOy -.register
5. x: lock cmpxchg src. dst
6. у: org x
7. byte OF3H.0Fh. op& Id
8. org у
9. ELSE
10. x: lock cmpxchgdst. src
11. y: orgx
12. byte 0F3H.0Fh. op&_st
13. orgy
14. ENDIF
15. UnDefineXMMxRegs
16. endm

Центральное место в макроопределении ХММ1 d_st_f3 занимают команда целочисленного устройства (в данном случае — CMPXCHG) и директива ORG. Первое действие данной макрокоманды — выяснить тип операнда приемника (dst) в макрокоманде MOVSS, так как он может быть и регистром, и ячейкой памяти. Это необходимо для правильного определения кода операции, которая будет управлять направлением потока данных. После того как определен приемник данных, с помощью условного перехода осуществляется переход на ветвь программы, где будет выполняться собственно формирование соответствующего ХММ-команде
MOVSS кода операции.
Формирование кода операции ХММ-команды MOVSS производится с помощью директивы org, которая предназначена для изменения значения счетчика адреса. В строках 6 или 11 директива org устанавливает значение счетчика адреса равным адресу метки х. Адрес метки х является адресом первого байта машинного кода команды CMPXCHG. Директива db в следующих строках размещает по этому адресу байтовые значения 0F3H,0Fh, ор&_1 d или 0F3H,0Fh, op&st, в зависимости от того, какое действие производится — загрузка (_ld) или сохранение (_st). Значение opc_Movss, с помощью которого формируются значения op&_st и ор&_1 d, определены в начале файла iaxmm.inc:

opcjtovssjd - 010Н
opc_Movss_st - 011H

Для дотошных читателей заметим еще один характерный момент. Для его полного понимания необходимо хорошо представлять себе формат машинной команды и назначение его полей. Достаточно полная информация об этом приведена в литературе [39, 40]. Обратите внимание на порядок следования операндов в заголовке макрокоманды, который построен по обычной для команд ассемблера схеме: коп назначение, источник. В команде CMPXCHG порядок обратный. Этого требует синтаксис команды. Это хорошо поясняет назначение бита d во втором байте кода операции, который характеризует направление передачи данных в микропроцессор (то есть в регистр) или в память (из микропроцессора (регистра)). Вы можете провести эксперимент. Проанализируйте машинные коды команды MOV:

Команды с непосредственным операндом:
CMPPS RXMM1. RXMM2/ml28, 18 CMPSS RXMM1, RXMM2/m32. i8 Однооперандные команды: FXRSTOR m512 FXSAVE m512 LDMXCSR m32 STMXCSR m32

Из перечисленных выше групп команд можно вывести следующую обобщенную структуру команды:

метка: код_операции операнд1. операнд2, операндЗ] ;текст комментария

Данная структура почти совпадает со структурой обычных команд ассемблера. В соответствии с общими принципами трансляции препроцессор будет работать с исходной программой в несколько этапов.

1. Лексический анализ (сканирование) исходного текста.
2. Синтаксический анализ.
3. Генерация кода.

Необходимо отметить, что по принципу действия разрабатываемый нами препроцессор относится к интерпретаторам. Читатель наверняка понимает, в чем состоит разница между интерпретатором и компилятором. Объект для работы компилятора — исходный текст программы в полном объеме. Выход компилятора — объектный модуль, то есть машинное представление исходной программы, пригодное для компоновки с другими модулями или получения исполняемого модуля. Интерпретатор работает с отдельными строками исходной программы. Распознав синтаксическую правильность строки, интерпретатор исполняет ее. В частности, интерпретация характерна для обработки входных строк командного процессора. Поэтому на примере данной задачи читатель может научиться достаточно профессионально организовывать языковое взаимодействие с пользователями своих программ.
В главе 2 описаны основные шаги разработки компилятора. Для интерпретатора разница невелика, в чем мы убедимся ниже.
Для распознавания лексем входной программы разработаем сканер, следуя для этого следующему алгоритму.

1. Выделить классы лексем.
2. Определить классы литер.
3. Определить условия выхода из сканера для каждого класса лексем.
4. Каждому классу лексем поставить в соответствие грамматику класса 3.
5. Для каждой грамматики, построенной на шаге 4, построить конечный автомат, который будет распознавать лексему данного класса.
6. Выполнить объединение («склеивание») конечных автоматов для всех классов лексем.
7. Составить матрицу переходов для «склеенного» конечного автомата.
8. «Навесить» семантику на дуги «склеенного» конечного автомата.
9. Выбрать коды лексической свертки для терминалов грамматики и формат таблицы идентификаторов.
10. Разработать программу сканера.

Язык описания команд ассемблера

Множество команд ассемблера можно описать с помощью следующего языка:

ASM_LENG={
Vt=(+ - AL АН BL BH CL CH DL DH AX EAX BX EBX CX ECX DX EDX BP EBP SP ESP DI EDI SI ESI BYTE SBYTE WORD SWORD DWORD SDWORD FWORD QWORD TBYTE REAL4 REAL8 REAL10 0 12 3 4 56789abcdefABCDEF NEAR16 NEAR32 FAR16 FAR32 AND NOT HIGH LOW HIGHWORO LOWWORD OFFSET SEG LROFFSET TYPE THIS PTR :.{)[] WIDTH MASK SIZE SIZEOF LENGTH LENGTHOF ST SHORT .TYPE OPATTR . название_команды * / MOD NEAR FAR OR XOR " 'hoqt у H 0 Q T Y { } < > :; EQ NE LT LE GT GE CS DS ES FS GS SS SHR SHL CRO CR2 CR3 DRO DR1 DR2 DR3 DR6 DR7 TR3 TR4 TR5 TR6 TR7 А5СП_символ_буква любой_символ_кроме_кавычки). Vn-( addOp asmlnstruction byteRegister constant constExpr dataType decdigit digits distance expr exprtist Expr eOl eO2 eO3 eO4 eO5 eO6 eO7 eO8 eO9 eOlO eOll hexdigit id mnemonic mulOp nearfar radixOverride orOp oldRecordFieldList relOp recordConst recordFieldList register shiftOp sizeArg string type segmentRegister specialRegister stext string stringChar structTag quote type typeld unionTag). P.
Z=(<asmlnstruction>) }

Множество правил Р грамматики ASM_LENG выглядит следующим образом:

За основу языка ASMLENG было взято описание языка MASM (из документации на него), ассемблер, поддерживаемый TASM, незначительно отличается от этого описания (в основном это касается некоторых операторов, типа OPATTR). Подчеркнем тот факт, что язык ASMLENG описывает лишь правило построения команд ассемблера, не затрагивая синтаксиса всей программы ассемблера в целом. Все строки, не являющиеся командами, будут просто игнорироваться и включаться в выходной файл в своем изначальном виде.

Выделение классов лексем

Для грамматики языка ASMLENG можно определить следующие классы лексем:

идентификатор — id; ключевые слова - AL АН BL ВН CL СН DL DH АХ ЕАХ ВХ ЕВХ СХ ЕСХ DX EDX ВР ЕВР SP ESP DI EDI SI ESI BYTE SBYTE WORD SWORD DWORD SDWORD FWORD QWORD TBYTE REAL4 REAL8 REAL10 NEAR16 NEAR32 FAR16 FAR32 AND NOT HIGH LOW HIGHWORD LOWWORD OFFSET SEG LROFFSET TYPE THIS PTR WIDTH MASK SIZE SIZEOF LENGTH LENGTHOF ST SHORT .TYPE OPATTR MOD NEAR FAR OR XOR EQ NE LT LE GT GE CS DS ES FS GS SS SHR SHL CRO CR2 CR3 DRO DR1 DR2 DR3 DR6 DR7 TR3 TR4 TR5 TR6 TR7 на-звание_команды; целые числа (константы) — 0123456789abcdefABCDEF; однолитерные разделители — +-/: . ()[] ,*" ' {}<>hoqtyHOQ Т Y; двулитерный разделитель — ;; символьные строки — А5СП_символ_буква, любой_символ_кроме_кавычки.

Классы литер

В случае грамматики языка ASMLENG можно определить следующие классы литер:

б — цифра; 1 — буква; b — литеры, которые игнорируются (к ним отнесем пробел); ¦ . si - одиночные разделители: + -/:.()[],*"'{}<>;; s2 — двулитерный разделитель: ;;.

Определение условий выхода из сканера для каждого класса лексем
Для каждого класса лексем определим условия, при которых сканер переходит в конечное состояние:

для идентификаторов — появление во входном потоке сканера любого символа, отличного от d (цифра) или 1 (буква); ключевые слова — появление пробела и нахождение соответствия введенной лексемы одному из ключевых слов языка; целые числа (константы) — появление любого символа, отличного от d; однолитерные разделители — появление любого символа; двулитерные разделители — появление любого символа; ,;;.
символьные строки — появление завершающей кавычки. ......г.

Построение автоматных грамматик для выделенных классов лексем
Для каждого класса лексем строится отдельная автоматная грамматика, соответствующая грамматике типа 3 по Хомско.му. В нашем случае набор таких грамматик может выглядеть так, как показано ниже:

идентификаторы — id, к которым по принципу построения можно отнести и ключевые слова — название_команды:

id=>ASCII_CMMBon_6yKea | id
ASCII_символ_буква | id decdigit :,; decdigit ^ 0|l|2|...8|9

целые числа — chint:

digits => decdigit | digits decdigit | digits hexdigit decdigit =>0|l|2|3|4|5|6|7|8|9 ¦

Oднолитерные разделители — +-/:.()[]. *"¦'---

SEPiL^. . | . | : |: | + | - | * I 4 ) / I L I ] Г Г I

двулитерный разделитель — ;;:

SEP2L=> : Q

«Склеивание» конечных автоматов для всех классов лексем

Мы не будем пытаться получить склеенный автомат, учитывающий все возможные случаи синтаксиса строки с командой ассемблера. Попытаемся получить объединенный конечный автомат для анализа типичной строки программы с ХММ-командой. С учетом этих упрощений «склеенный» конечный автомат может выглядеть так, как показано на рис. 10.2.

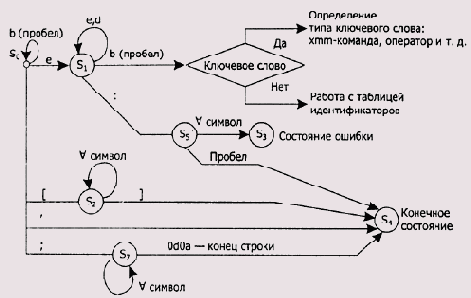
Рис. 10.2. Упрощенный вариант «склеенного» конечного автомата

Для представленного на рисунке склеенного конечного автомата таблица (матрица) переходов показана ниже.

L D [ ] пробел
SO SI S2 S4 S4 SO S6
SI SI SI S5 S4
со S2 S2 S4
S3

S4
S5 S3 S3 S3 S3 S3 S3 S4
S6 SG S6 S6 S6 S6 S6 S6 S6

Как обычно, два из этих состояний являются конечными:

S3 — состояние ошибки; S4 — конечное состояние.

Состояние S6 — состояние, соответствующее комментарию, то есть допустимы любые символы. Ограничение комментария — конец строки. Строки в таблице переходов соответствуют состояниям склеенного конечного автомата, основа столбцов — классы лексем. Логика работы сканера с использованием таблицы переходов описана в главе 2.
После заполнения таблицы переходов можно навешивать семантику на « дуги» переходов из одного состояния в другое. Основная задача при этом — не брать на себя ничего лишнего. Главное — локализовать поле с названием команды, определить принадлежность ее к группе ХММ-команд. Если это не так, то дальней
ший процесс сканирования строки можно прекращать, копировать ее в выходной поток (пусть транслятор ассемблера разбирается с ней сам) и переходить к анализу очередной строки исходного текста ассемблерной программы.
В самом простом случае нашу задачу можно решить легко — в очередной строке выделить метку, если она есть, затем выделить название команды, и если она является ХММ-командой, то продолжить обработку строки. Если очередная строка не является ХММ-командой, то копируем ее полностью в выходной файл. Если очередная строка — ХММ-команда, то локализуем операнды и определяем их тип. По крайней мере один из операндов должен быть регистром. Если строка синтаксически верна для конкретной ХММ-команды, то формируем ее аналог, понятный для восприятия используемым нами транслятором ассемблера. Этот процесс может быть похожим на первый способ формирования ХММ-команд с помощью включаемого файла iaxmm.inc.

Синтаксический анализ

Если веденная строка исходной программы является строкой с ХММ-командой, то необходимо получить ее лексическую свертку для проведения синтаксической проверки и подготовки к дальнейшему преобразованию. Здесь простор для творческих изысканий весьма велик. Поэтому мы не будем повторять соответствующий материал главы 2, а обратимся к тексту программы, который выполняет такое преобразование. Его описание содержит множество технических подробностей, не относящихся к предмету книги. По этой причине программа-препроцессор с соответствующими пояснениями деталей реализации вынесена на дискету, прилагаемую к книге. Протестировать эту программу вы можете на примерах программ с ХММ-командами, приведенными в первой части данной главы.